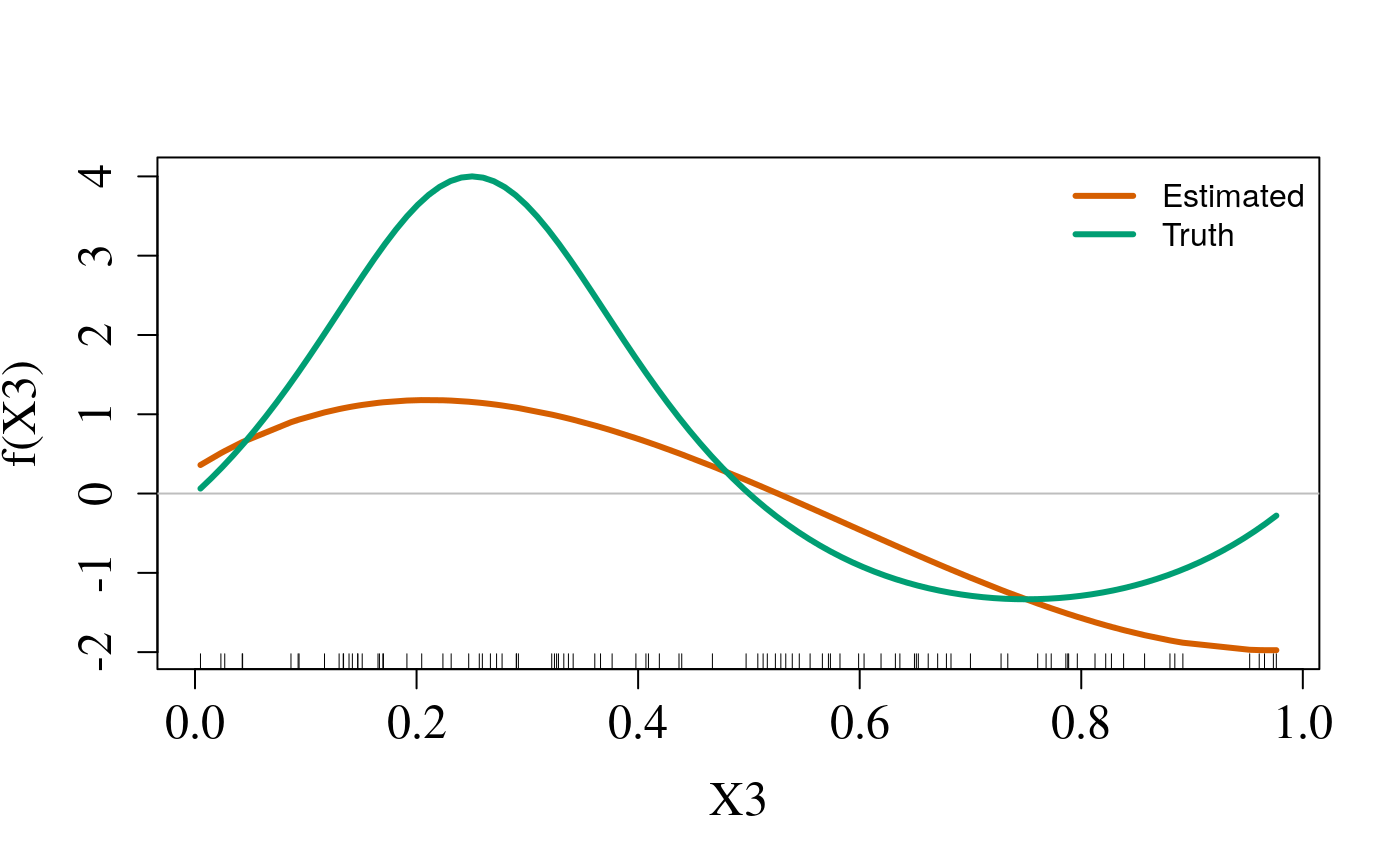
Introduction to the sail package

sail is a package that fits a linear model with non-linear interactions via penalized maximum likelihood. The regularization path is computed at a grid of values for the regularization parameter \(\lambda\) and a fixed value of the second regularization parameter \(\alpha\). The method enforces the strong heredity property, i.e., an interaction is selected only if its corresponding main effects are also included. The interactions are limited to a single exposure variable, i.e., \(y \sim e + x_1 + x_2 + e*x_1 + e*x_2 + \epsilon\). Furthermore, this package allows a user-defined basis expansion on the \(x\) variables to allow for non-linear effects. The default is bsplines (e.g. splines::bs(x, 5)). It currently only fits linear models (binomial models are due in the next release).

Model

Let \(Y=(Y_1, \ldots, Y_n) \in \mathbb{R}^n\) be a continuous outcome variable, a binary or continuous environment vector, a matrix of predictors, and \(\varepsilon = (\varepsilon_1, \ldots, \varepsilon_n) \in \mathbb{R}^n\) a vector of i.i.d random variables with mean 0. Furthermore let \(f_j: \mathbb{R} \rightarrow \mathbb{R}\) be a smoothing method for variable \(X_j\) by a projection on to a set of basis functions: \[\begin{equation} f_j(X_j) = \sum_{\ell = 1}^{m_j} \psi_{j\ell}(X_j) \beta_{j\ell} \label{eq:smooth} \end{equation}\] Here, the \(\left\lbrace \psi_{j\ell} \right\rbrace_1^{m_j}\) are a family of basis functions in \(X_j\)~. Let \(\boldsymbol{\Psi}_j\) be the \(n \times m_j\) matrix of evaluations of the \(\psi_{j\ell}\) and for \(j = 1, \ldots, p\), i.e., \(\boldsymbol{\theta}_j\) is a \(m_j\)-dimensional column vector of basis coefficients for the \(j\)th main effect. In this article we consider an additive interaction regression model of the form \[\begin{align} Y & = \beta_0 \cdot \boldsymbol{1} + \sum_{j=1}^p \boldsymbol{\Psi}_j \boldsymbol{\theta}_j + \beta_E X_E + \sum_{j=1}^p (X_E \circ \boldsymbol{\Psi}_j) \boldsymbol{\alpha}_{j} + \varepsilon \label{eq:linpred} \end{align}\] where \(\beta_0\) is the intercept, \(\beta_E\) is the coefficient for the environment variable, \(\boldsymbol{\alpha}_j = (\alpha_{j1}, \ldots, \alpha_{jm_j})\in \mathbb{R}^{m_j}\) are the basis coefficients for the \(j\)th interaction term and \((X_E \circ \boldsymbol{\Psi}_j)\) is the \(n \times m_j\) matrix formed by the component-wise multiplication of the column vector \(X_E\) by each column of \(\boldsymbol{\Psi}_j\). To enforce the strong heredity property, we reparametrize the coefficients for the interaction terms in~ as \(\boldsymbol{\alpha}_{j} = \gamma_{j} \beta_E \boldsymbol{\theta}_j\): \[\begin{align} Y & = \beta_0 \cdot \boldsymbol{1} + \sum_{j=1}^p \boldsymbol{\Psi}_j \boldsymbol{\theta}_j + \beta_E X_E + \sum_{j=1}^p \gamma_{j} \beta_E (X_E \circ \boldsymbol{\Psi}_j) \boldsymbol{\theta}_j + \varepsilon \label{eq:linpred2} \end{align}\] For a continuous response, we use the squared-error loss: \[\begin{equation} \mathcal{L}(Y;\boldsymbol{\theta}) = \frac{1}{2n}\lVert Y - \beta_0 \cdot \boldsymbol{1} - \sum_{j=1}^p \boldsymbol{\Psi}_j \boldsymbol{\theta}_j - \beta_E X_E - \sum_{j=1}^p \gamma_{j} \beta_E (X_E \circ \boldsymbol{\Psi}_j) \boldsymbol{\theta}_j \rVert_2^2 \end{equation}\] where \(\boldsymbol{\theta} \equiv (\beta_0, \beta_E,\boldsymbol{\theta}_1, \ldots, \boldsymbol{\theta}_p, \gamma_1, \ldots, \gamma_p)\).

We consider the following penalized least squares criterion for this problem: \[\begin{equation} \arg\min_{\boldsymbol{\theta} } \mathcal{L}(Y;\boldsymbol{\theta}) + \lambda (1-\alpha) \left( w_E |\beta_E| + \sum_{j=1}^{p} w_j \lVert\boldsymbol{\theta}_j \rVert_2 \right) + \lambda\alpha \sum_{j=1}^{p} w_{jE} |\gamma_{j}| \label{eq:lassolikelihood3} \end{equation}\] where \(\lambda >0\) and \(\alpha \in (0,1)\) are tuning parameters and \(w_E, w_j, w_{jE}\) are adaptive weights for \(j=1, \ldots, p\). These weights serve as a way of allowing parameters to be penalized differently.

Installation

The package can be installed from GitHub via

install.packages("pacman")
pacman::p_load_gh('sahirbhatnagar/sail')

Quick Start

We give a quick overview of the main functions and go into details in other vignettes. We will use the simulated data which ships with the package and can be loaded via:

library(sail)
data("sailsim")
names(sailsim)
#> [1] "x"        "y"        "e"        "f1"       "f2"       "f3"      
#> [7] "f4"       "f3.inter" "f4.inter"

We first define a basis expansion. In this example we use cubic bsplines with degree 3.

library(splines)
f.basis <- function(x) splines::bs(x, degree = 3)

Next we fit the model using the most basic call to sail

fit <- sail(x = sailsim$x, y = sailsim$y, e = sailsim$e, basis = f.basis)

fit is an object of class sail that contains all the relevant information of the fitted model including the estimated coefficients at each value of \(\lambda\) (by default the program chooses its own decreasing sequence of 100 \(\lambda\) values). There are print, plot, coef and predict methods of objects of class sail. The print method outputs the following:

fit
#> 
#> Call:  sail(x = sailsim$x, y = sailsim$y, e = sailsim$e, basis = f.basis) 
#> 
#>      df_main df_interaction df_environment     %Dev  Lambda
#> s1         0              0              0 0.000000 1.48800
#> s2         0              0              1 0.001701 1.42000
#> s3         0              0              1 0.003359 1.35600
#> s4         0              0              1 0.004899 1.29400
#> s5         0              0              1 0.006354 1.23500
#> s6         0              0              1 0.007728 1.17900
#> s7         0              0              1 0.009028 1.12600
#> s8         0              0              1 0.010260 1.07500
#> s9         1              0              1 0.018970 1.02600
#> s10        2              0              1 0.042490 0.97900
#> s11        2              0              1 0.069000 0.93450
#> s12        2              0              1 0.094110 0.89210
#> s13        2              0              1 0.117900 0.85150
#> s14        2              0              1 0.140500 0.81280
#> s15        3              0              1 0.163800 0.77590
#> s16        4              0              1 0.189100 0.74060
#> s17        4              0              1 0.214000 0.70690
#> s18        5              0              1 0.238100 0.67480
#> s19        5              0              1 0.262200 0.64410
#> s20        3              1              1 0.439100 0.61490
#> s21        4              2              1 0.457000 0.58690
#> s22        5              2              1 0.475400 0.56020
#> s23        5              2              1 0.491600 0.53480
#> s24        5              2              1 0.505300 0.51050
#> s25        5              2              1 0.518200 0.48730
#> s26        5              2              1 0.530100 0.46510
#> s27        5              2              1 0.541200 0.44400
#> s28        5              2              1 0.551400 0.42380
#> s29        5              2              1 0.561400 0.40450
#> s30        5              2              1 0.569300 0.38620
#> s31        5              2              1 0.577300 0.36860
#> s32        6              2              1 0.585500 0.35190
#> s33        6              2              1 0.594900 0.33590
#> s34        6              2              1 0.603700 0.32060
#> s35        7              3              1 0.612300 0.30600
#> s36        7              3              1 0.620400 0.29210
#> s37        8              4              1 0.629200 0.27880
#> s38        8              4              1 0.641900 0.26620
#> s39        9              4              1 0.650000 0.25410
#> s40        9              4              1 0.658500 0.24250
#> s41        8              4              1 0.689000 0.23150
#> s42        8              4              1 0.695300 0.22100
#> s43        8              4              1 0.701400 0.21090
#> s44        9              4              1 0.707200 0.20130
#> s45        8              6              1 0.728900 0.19220
#> s46        8              6              1 0.733700 0.18350
#> s47        8              6              1 0.738200 0.17510
#> s48        8              7              1 0.742400 0.16720
#> s49        9              7              1 0.747600 0.15960
#> s50       10              7              1 0.752100 0.15230
#> s51       10              7              1 0.756500 0.14540
#> s52       10              7              1 0.760900 0.13880
#> s53       11              7              1 0.765200 0.13250
#> s54       11              7              1 0.769900 0.12640
#> s55       11              7              1 0.773900 0.12070
#> s56       11              7              1 0.778100 0.11520
#> s57       12              9              1 0.794000 0.11000
#> s58       12              9              1 0.798500 0.10500
#> s59       12              9              1 0.802700 0.10020
#> s60       12              9              1 0.806600 0.09565
#> s61       13              9              1 0.810400 0.09131
#> s62       13              9              1 0.814100 0.08716
#> s63       13              9              1 0.817200 0.08319
#> s64       16              9              1 0.820000 0.07941
#> s65       16              9              1 0.822900 0.07580
#> s66       16              9              1 0.825600 0.07236
#> s67       16              9              1 0.828200 0.06907
#> s68       16              9              1 0.830700 0.06593
#> s69       17             10              1 0.833500 0.06293
#> s70       17             10              1 0.840000 0.06007
#> s71       16             12              1 0.849000 0.05734
#> s72       16             12              1 0.851400 0.05474
#> s73       18             12              1 0.853900 0.05225
#> s74       19             12              1 0.856700 0.04987
#> s75       19             12              1 0.859600 0.04761
#> s76       19             12              1 0.862600 0.04544
#> s77       19             15              1 0.897700 0.04338
#> s78       20             18              1 0.907600 0.04141
#> s79       20             18              1 0.909800 0.03952
#> s80       20             19              1 0.925800 0.03773
#> s81       20             20              1 0.927700 0.03601
#> s82       20             20              1 0.929700 0.03438
#> s83       20             20              1 0.931800 0.03281
#> s84       20             20              1 0.934500 0.03132
#> s85       20             20              1 0.936100 0.02990
#> s86       20             20              1 0.937700 0.02854
#> s87       20             20              1 0.939300 0.02724
#> s88       20             20              1 0.943900 0.02600
#> s89       20             20              1 0.944700 0.02482
#> s90       20             20              1 0.945600 0.02369
#> s91       20             20              1 0.946500 0.02262
#> s92       20             20              1 0.947100 0.02159
#> s93       20             20              1 0.948500 0.02061
#> s94       20             20              1 0.949200 0.01967
#> s95       20             20              1 0.950100 0.01878
#> s96       20             20              1 0.950700 0.01792
#> s97       20             20              1 0.951400 0.01711
#> s98       20             20              1 0.952000 0.01633
#> s99       20             20              1 0.952600 0.01559
#> s100      20             20              1 0.954900 0.01488

When expand = TRUE (i.e. the user did not provide their own design matrix), the df_main and df_interaction columns correspond to the number of non-zero predictors present in the model before basis expansion. This does not correspond to the number of non-zero coefficients in the model, but rather the number of unique variables. In this example we expanded each column of \(\mathbf{X}\) to five columns. If df_main=4, df_interaction=2 and df_environment=1, then the total number of non-zero coefficients would be \(5 \times (4+2) + 1\).

The entire solution path can be plotted via the plot method for objects of class sail. The y-axis is the value of the coefficient and the x-axis is the \(\log(\lambda)\). Each line represents a coefficient in the model, and each color represents a variable (i.e. in this example a given variable will have 5 lines when it is non-zero). The numbers at the top of the plot represent the number of non-zero variables in the model: top panel (df_main + df_environment), bottom panel (df_interaction). The black line is the coefficient path for the environment variable.

plot(fit)

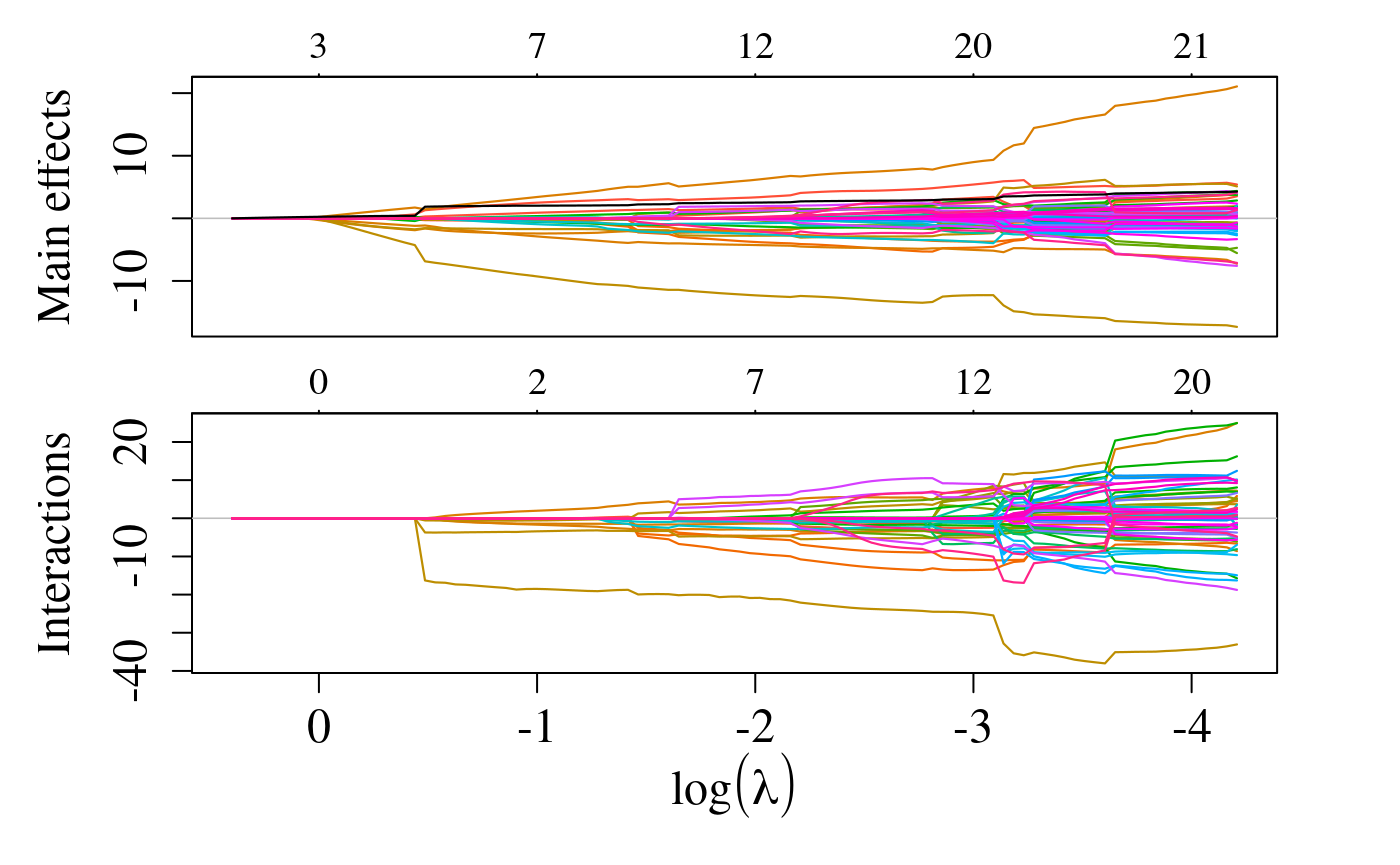
The estimated coefficients at each value of lambda is given by (matrix partially printed here for brevity)

coef(fit)[1:6,50:55]
#> 6 x 6 sparse Matrix of class "dgCMatrix"
#>                    s50        s51        s52        s53       s54
#> (Intercept)  5.3445152  5.3350735  5.3260684  5.3209183  5.314509
#> X1_1         0.7668023  0.8407632  0.9134418  0.9963138  1.085707
#> X1_2         1.4682908  1.5072192  1.5402298  1.5855723  1.652733
#> X1_3         3.1982020  3.2553440  3.3051339  3.3837769  3.485491
#> X2_1        -3.5192313 -3.6285818 -3.7307130 -3.8183660 -3.881222
#> X2_2        -1.8958170 -1.8899979 -1.8853574 -1.8738510 -1.860779
#>                   s55
#> (Intercept)  5.310267
#> X1_1         1.173776
#> X1_2         1.705634
#> X1_3         3.572614
#> X2_1        -3.949365
#> X2_2        -1.845185

The predicted response at each value of lambda:

predict(fit)[1:5,50:55]
#>             s50        s51        s52        s53        s54        s55
#> [1,]  5.7445034  5.7179456  5.6497326  5.6215581  5.5483312  5.5167354
#> [2,]  3.5886152  3.6608123  3.6673009  3.7788863  3.8397710  3.9364845
#> [3,]  0.7525327  0.7083256  0.6460716  0.6605192  0.6352286  0.6510435
#> [4,] 12.5038372 12.4852941 12.5806330 12.5278481 12.5857507 12.5421780
#> [5,]  1.3865576  1.3339420  1.3466244  1.3138336  1.3409284  1.3203384

The predicted response at a specific value of lambda can be specified by the s argument:

predict(fit, s = 0.8)
#>               1
#>   [1,] 5.565188
#>   [2,] 5.245648
#>   [3,] 4.256588
#>   [4,] 6.314703
#>   [5,] 3.884374
#>   [6,] 4.446973
#>   [7,] 6.112132
#>   [8,] 5.360375
#>   [9,] 5.972536
#>  [10,] 5.558947
#>  [11,] 5.252652
#>  [12,] 6.394977
#>  [13,] 6.304268
#>  [14,] 4.993944
#>  [15,] 6.673554
#>  [16,] 4.852025
#>  [17,] 5.011305
#>  [18,] 4.855807
#>  [19,] 5.182772
#>  [20,] 5.292666
#>  [21,] 5.939055
#>  [22,] 5.624398
#>  [23,] 4.496055
#>  [24,] 6.156093
#>  [25,] 4.839130
#>  [26,] 6.202291
#>  [27,] 6.240929
#>  [28,] 4.440300
#>  [29,] 6.173744
#>  [30,] 5.779888
#>  [31,] 5.060847
#>  [32,] 5.034286
#>  [33,] 6.319719
#>  [34,] 4.387120
#>  [35,] 6.716587
#>  [36,] 5.668114
#>  [37,] 5.065923
#>  [38,] 4.961400
#>  [39,] 5.008489
#>  [40,] 5.146974
#>  [41,] 3.696416
#>  [42,] 4.303783
#>  [43,] 5.580174
#>  [44,] 6.591266
#>  [45,] 4.633462
#>  [46,] 4.522579
#>  [47,] 5.633387
#>  [48,] 6.633019
#>  [49,] 5.013153
#>  [50,] 5.267268
#>  [51,] 5.035807
#>  [52,] 4.611586
#>  [53,] 5.341352
#>  [54,] 5.233311
#>  [55,] 4.733031
#>  [56,] 5.022145
#>  [57,] 5.299347
#>  [58,] 5.187987
#>  [59,] 6.093533
#>  [60,] 5.332161
#>  [61,] 4.536252
#>  [62,] 3.800441
#>  [63,] 6.222930
#>  [64,] 4.917357
#>  [65,] 5.080531
#>  [66,] 5.868890
#>  [67,] 4.541408
#>  [68,] 5.701353
#>  [69,] 5.271430
#>  [70,] 6.208581
#>  [71,] 4.813133
#>  [72,] 4.031251
#>  [73,] 5.693444
#>  [74,] 6.269703
#>  [75,] 4.328094
#>  [76,] 5.015667
#>  [77,] 4.140977
#>  [78,] 5.788631
#>  [79,] 5.137175
#>  [80,] 5.144183
#>  [81,] 5.533654
#>  [82,] 5.638968
#>  [83,] 5.349115
#>  [84,] 5.995233
#>  [85,] 4.787946
#>  [86,] 4.485989
#>  [87,] 4.589191
#>  [88,] 5.084970
#>  [89,] 4.414470
#>  [90,] 3.896057
#>  [91,] 5.675552
#>  [92,] 6.268628
#>  [93,] 5.593670
#>  [94,] 5.971994
#>  [95,] 5.096703
#>  [96,] 4.168302
#>  [97,] 5.017025
#>  [98,] 5.368094
#>  [99,] 4.576291
#> [100,] 5.764786

You can specify more than one value for s:

predict(fit, s = c(0.8, 0.2))
#>               1          2
#>   [1,] 5.565188  6.4563490
#>   [2,] 5.245648  3.5762830
#>   [3,] 4.256588  1.2541443
#>   [4,] 6.314703 12.3815143
#>   [5,] 3.884374  1.5612304
#>   [6,] 4.446973  1.5503816
#>   [7,] 6.112132 12.6330145
#>   [8,] 5.360375  6.4671028
#>   [9,] 5.972536  7.0190070
#>  [10,] 5.558947  5.2948898
#>  [11,] 5.252652  4.3677887
#>  [12,] 6.394977 11.2278283
#>  [13,] 6.304268 11.6189806
#>  [14,] 4.993944  4.0124434
#>  [15,] 6.673554 14.4290841
#>  [16,] 4.852025  5.0443558
#>  [17,] 5.011305  0.8168762
#>  [18,] 4.855807  4.5902225
#>  [19,] 5.182772  3.1477565
#>  [20,] 5.292666  3.4902000
#>  [21,] 5.939055  8.4361272
#>  [22,] 5.624398  4.6555593
#>  [23,] 4.496055  1.7045694
#>  [24,] 6.156093 10.5558726
#>  [25,] 4.839130  1.2444600
#>  [26,] 6.202291  8.6260313
#>  [27,] 6.240929  7.7126054
#>  [28,] 4.440300 -0.7778888
#>  [29,] 6.173744 12.0720146
#>  [30,] 5.779888  1.8831854
#>  [31,] 5.060847  4.9276303
#>  [32,] 5.034286  8.3934198
#>  [33,] 6.319719  8.9647247
#>  [34,] 4.387120  3.6730133
#>  [35,] 6.716587 15.4640443
#>  [36,] 5.668114  1.1145380
#>  [37,] 5.065923  5.0030880
#>  [38,] 4.961400  3.0886490
#>  [39,] 5.008489  3.5325687
#>  [40,] 5.146974  4.7369669
#>  [41,] 3.696416  1.7665100
#>  [42,] 4.303783  0.7109199
#>  [43,] 5.580174  6.8465242
#>  [44,] 6.591266 14.7008154
#>  [45,] 4.633462  2.1878324
#>  [46,] 4.522579  3.8488986
#>  [47,] 5.633387  6.2435977
#>  [48,] 6.633019 16.8729068
#>  [49,] 5.013153  3.0090785
#>  [50,] 5.267268  7.7524439
#>  [51,] 5.035807  5.7762293
#>  [52,] 4.611586  1.7242234
#>  [53,] 5.341352  7.2133769
#>  [54,] 5.233311  8.9233017
#>  [55,] 4.733031  2.0904075
#>  [56,] 5.022145  1.2321963
#>  [57,] 5.299347  5.5841592
#>  [58,] 5.187987  8.1850179
#>  [59,] 6.093533  9.1272205
#>  [60,] 5.332161  2.6762385
#>  [61,] 4.536252  1.2714320
#>  [62,] 3.800441 -0.7821244
#>  [63,] 6.222930  9.0399619
#>  [64,] 4.917357  1.4590598
#>  [65,] 5.080531  3.3498113
#>  [66,] 5.868890  3.2462364
#>  [67,] 4.541408  3.8775236
#>  [68,] 5.701353  5.9176470
#>  [69,] 5.271430  9.4635363
#>  [70,] 6.208581  8.5531857
#>  [71,] 4.813133  3.1399498
#>  [72,] 4.031251  0.8587915
#>  [73,] 5.693444  7.2551243
#>  [74,] 6.269703  4.7373189
#>  [75,] 4.328094  2.7418860
#>  [76,] 5.015667  1.4436768
#>  [77,] 4.140977  2.3070947
#>  [78,] 5.788631 16.4559530
#>  [79,] 5.137175  7.0246294
#>  [80,] 5.144183  2.3912821
#>  [81,] 5.533654  4.2128178
#>  [82,] 5.638968  4.5853076
#>  [83,] 5.349115  5.3680719
#>  [84,] 5.995233  5.6151668
#>  [85,] 4.787946  3.5272371
#>  [86,] 4.485989  2.9988064
#>  [87,] 4.589191  3.5070799
#>  [88,] 5.084970  1.7410672
#>  [89,] 4.414470  4.7618966
#>  [90,] 3.896057  5.6814850
#>  [91,] 5.675552  8.0216272
#>  [92,] 6.268628  9.1200249
#>  [93,] 5.593670  4.7429260
#>  [94,] 5.971994  7.6268458
#>  [95,] 5.096703  5.7827835
#>  [96,] 4.168302  2.7426953
#>  [97,] 5.017025  9.8201852
#>  [98,] 5.368094  6.1535859
#>  [99,] 4.576291  3.9789271
#> [100,] 5.764786  4.7680511

You can also extract a list of active variables (i.e. variables with a non-zero estimated coefficient) for each value of lambda:

fit[["active"]]
#> [[1]]
#> character(0)
#> 
#> [[2]]
#> [1] "E"
#> 
#> [[3]]
#> [1] "E"
#> 
#> [[4]]
#> [1] "E"
#> 
#> [[5]]
#> [1] "E"
#> 
#> [[6]]
#> [1] "E"
#> 
#> [[7]]
#> [1] "E"
#> 
#> [[8]]
#> [1] "E"
#> 
#> [[9]]
#> [1] "X3" "E" 
#> 
#> [[10]]
#> [1] "X3" "X4" "E" 
#> 
#> [[11]]
#> [1] "X3" "X4" "E" 
#> 
#> [[12]]
#> [1] "X3" "X4" "E" 
#> 
#> [[13]]
#> [1] "X3" "X4" "E" 
#> 
#> [[14]]
#> [1] "X3" "X4" "E" 
#> 
#> [[15]]
#> [1] "X1" "X3" "X4" "E" 
#> 
#> [[16]]
#> [1] "X1" "X3" "X4" "X8" "E" 
#> 
#> [[17]]
#> [1] "X1" "X3" "X4" "X8" "E" 
#> 
#> [[18]]
#> [1] "X1"  "X3"  "X4"  "X8"  "X11" "E"  
#> 
#> [[19]]
#> [1] "X1"  "X3"  "X4"  "X8"  "X11" "E"  
#> 
#> [[20]]
#> [1] "X1"   "X3"   "X4"   "X4:E" "E"   
#> 
#> [[21]]
#> [1] "X1"   "X3"   "X4"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[22]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[23]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[24]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[25]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[26]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[27]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[28]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[29]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[30]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[31]]
#> [1] "X1"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[32]]
#> [1] "X1"   "X2"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[33]]
#> [1] "X1"   "X2"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[34]]
#> [1] "X1"   "X2"   "X3"   "X4"   "X8"   "X11"  "X3:E" "X4:E" "E"   
#> 
#> [[35]]
#>  [1] "X1"   "X2"   "X3"   "X4"   "X8"   "X11"  "X14"  "X1:E" "X3:E" "X4:E"
#> [11] "E"   
#> 
#> [[36]]
#>  [1] "X1"   "X2"   "X3"   "X4"   "X8"   "X11"  "X14"  "X1:E" "X3:E" "X4:E"
#> [11] "E"   
#> 
#> [[37]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X14"   "X16"  
#>  [9] "X1:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[38]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X14"   "X16"  
#>  [9] "X1:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[39]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X14"   "X16"  
#>  [9] "X20"   "X1:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[40]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X14"   "X16"  
#>  [9] "X20"   "X1:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[41]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X2:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[42]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X2:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[43]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X2:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[44]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X14"   "X16"  
#>  [9] "X20"   "X2:E"  "X3:E"  "X4:E"  "X11:E" "E"    
#> 
#> [[45]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X11:E" "X16:E" "E"    
#> 
#> [[46]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X11:E" "X16:E" "E"    
#> 
#> [[47]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X11:E" "X16:E" "E"    
#> 
#> [[48]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X8"    "X11"   "X16"   "X20"  
#>  [9] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E"  "X11:E" "X16:E" "E"    
#> 
#> [[49]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X16"  
#>  [9] "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E"  "X11:E" "X16:E"
#> [17] "E"    
#> 
#> [[50]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E"  "X11:E"
#> [17] "X16:E" "E"    
#> 
#> [[51]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E"  "X11:E"
#> [17] "X16:E" "E"    
#> 
#> [[52]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E"  "X11:E"
#> [17] "X16:E" "E"    
#> 
#> [[53]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E" 
#> [17] "X11:E" "X16:E" "E"    
#> 
#> [[54]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E" 
#> [17] "X11:E" "X16:E" "E"    
#> 
#> [[55]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E" 
#> [17] "X11:E" "X16:E" "E"    
#> 
#> [[56]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X11"   "X14"  
#>  [9] "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X8:E" 
#> [17] "X11:E" "X16:E" "E"    
#> 
#> [[57]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X10"   "X11"  
#>  [9] "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [17] "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[58]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X10"   "X11"  
#>  [9] "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [17] "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[59]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X10"   "X11"  
#>  [9] "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [17] "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[60]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X6"    "X8"    "X10"   "X11"  
#>  [9] "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [17] "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[61]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X10"  
#>  [9] "X11"   "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E" 
#> [17] "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[62]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X10"  
#>  [9] "X11"   "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E" 
#> [17] "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[63]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X10"  
#>  [9] "X11"   "X14"   "X16"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E" 
#> [17] "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[64]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E"
#> [25] "X20:E" "E"    
#> 
#> [[65]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E"
#> [25] "X20:E" "E"    
#> 
#> [[66]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E"
#> [25] "X20:E" "E"    
#> 
#> [[67]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E"
#> [25] "X20:E" "E"    
#> 
#> [[68]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X11:E" "X16:E"
#> [25] "X20:E" "E"    
#> 
#> [[69]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X18"   "X19"  
#> [17] "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X9:E" 
#> [25] "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[70]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X12"   "X14"   "X15"   "X16"   "X18"   "X19"  
#> [17] "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X6:E"  "X8:E"  "X9:E" 
#> [25] "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[71]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X14"   "X15"   "X16"   "X18"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E"  "X6:E"  "X8:E"  "X9:E" 
#> [25] "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[72]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X8"    "X9"   
#>  [9] "X10"   "X11"   "X14"   "X15"   "X16"   "X18"   "X19"   "X20"  
#> [17] "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E"  "X6:E"  "X8:E"  "X9:E" 
#> [25] "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[73]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X13"   "X14"   "X15"   "X16"   "X18"  
#> [17] "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E"  "X6:E" 
#> [25] "X8:E"  "X9:E"  "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[74]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E" 
#> [25] "X6:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[75]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E" 
#> [25] "X6:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[76]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E" 
#> [25] "X6:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X16:E" "X20:E" "E"    
#> 
#> [[77]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X15"   "X16"   "X17"  
#> [17] "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E"  "X5:E" 
#> [25] "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X12:E" "X13:E" "X16:E"
#> [33] "X19:E" "X20:E" "E"    
#> 
#> [[78]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E" "E"    
#> 
#> [[79]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E" "E"    
#> 
#> [[80]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X19:E" "X20:E" "E"    
#> 
#> [[81]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[82]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[83]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[84]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[85]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[86]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[87]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[88]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[89]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[90]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[91]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[92]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[93]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[94]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[95]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[96]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[97]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[98]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[99]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"    
#> 
#> [[100]]
#>  [1] "X1"    "X2"    "X3"    "X4"    "X5"    "X6"    "X7"    "X8"   
#>  [9] "X9"    "X10"   "X11"   "X12"   "X13"   "X14"   "X15"   "X16"  
#> [17] "X17"   "X18"   "X19"   "X20"   "X1:E"  "X2:E"  "X3:E"  "X4:E" 
#> [25] "X5:E"  "X6:E"  "X7:E"  "X8:E"  "X9:E"  "X10:E" "X11:E" "X12:E"
#> [33] "X13:E" "X14:E" "X15:E" "X16:E" "X17:E" "X18:E" "X19:E" "X20:E"
#> [41] "E"

Cross-Validation

cv.sail is the main function to do cross-validation along with plot, predict, and coef methods for objects of class cv.sail. We can also run it in parallel:

set.seed(432) # to reproduce results (randomness due to CV folds)
library(doParallel) 
#> Loading required package: foreach
#> Loading required package: iterators
#> Loading required package: parallel
registerDoParallel(cores = 2) 
cvfit <- cv.sail(x = sailsim$x, y = sailsim$y, e = sailsim$e, basis = f.basis,
                 dfmax = 10, # to speed up vignette build time
                 nfolds = 5, parallel = TRUE, nlambda = 50)

We plot the cross-validated error curve which has the mean-squared error on the y-axis and \(\log(\lambda)\) on the x-axis. It includes the cross-validation curve (red dotted line), and upper and lower standard deviation curves along the \(\lambda\) sequence (error bars). Two selected \(\lambda\)’s are indicated by the vertical dotted lines (see below). The numbers at the top of the plot represent the total number of non-zero variables at that value of \(\lambda\) (df_main + df_environment + df_interaction):

plot(cvfit)

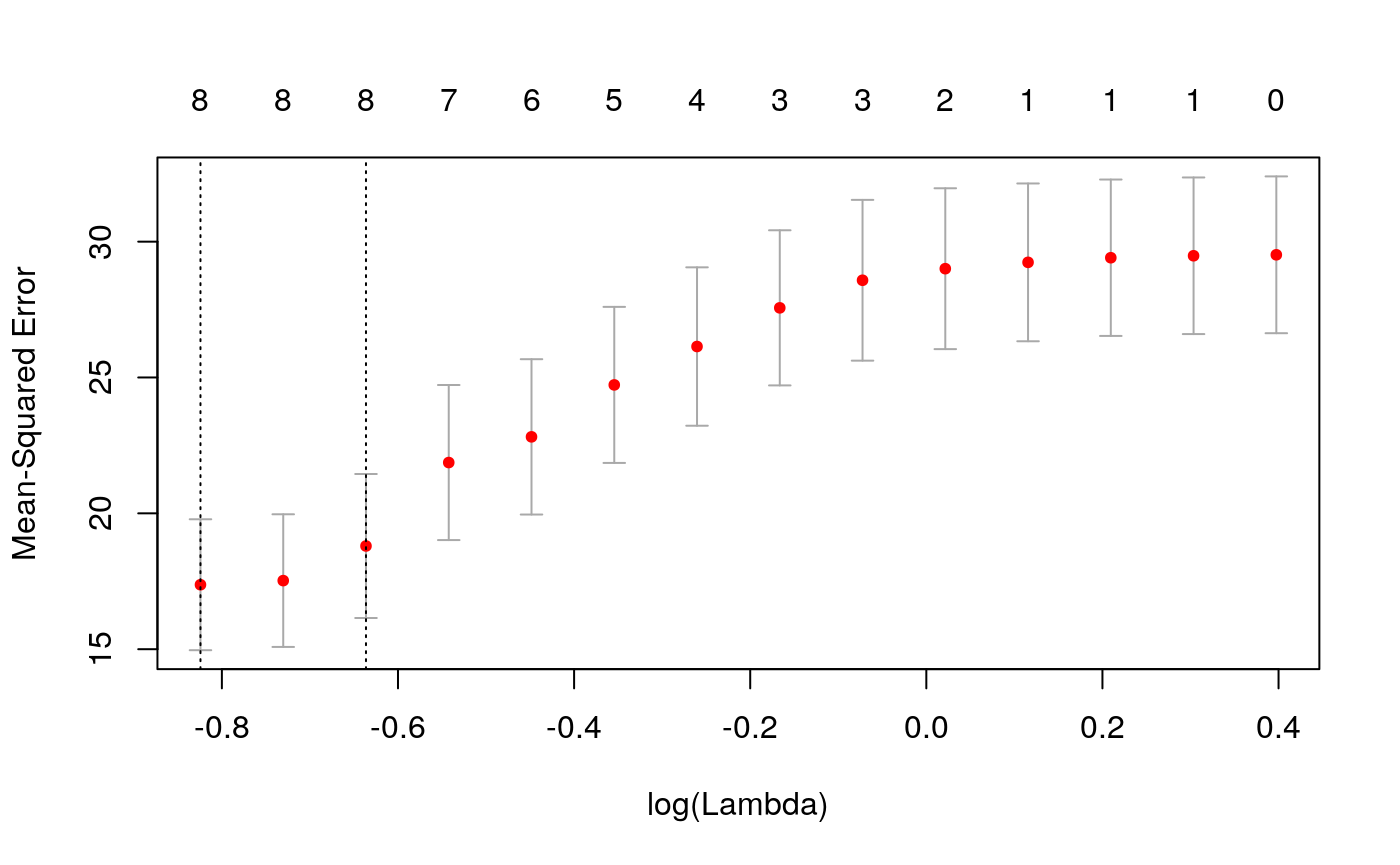
lambda.min is the value of \(\lambda\) that gives minimum mean cross-validated error. The other \(\lambda\) saved is lambda.1se, which gives the most regularized model such that error is within one standard error of the minimum. We can view the selected \(\lambda\)’s and the corresponding coefficients:

cvfit[["lambda.min"]]
#> [1] 0.4385394
cvfit[["lambda.1se"]]
#> [1] 0.5292261

The estimated coefficients at lambda.1se and lambda.min:

cbind(coef(cvfit, s="lambda.1se"), # lambda.1se is the default
coef(cvfit, s = "lambda.min"))
#> 122 x 2 sparse Matrix of class "dgCMatrix"
#>                        1           1
#> (Intercept)   5.44728244   5.4489968
#> X1_1         -0.33479902  -0.3475998
#> X1_2          0.46732277   0.6911858
#> X1_3          1.70401603   2.1622040
#> X2_1          .            .        
#> X2_2          .            .        
#> X2_3          .            .        
#> X3_1          2.12553380   2.7746062
#> X3_2         -1.81057790  -2.3950334
#> X3_3         -2.10280952  -2.3355539
#> X4_1         -0.26919665  -0.2769379
#> X4_2         -7.58248628  -8.4137355
#> X4_3         -1.62272272  -1.6547066
#> X5_1          .            .        
#> X5_2          .            .        
#> X5_3          .            .        
#> X6_1          .            .        
#> X6_2          .            .        
#> X6_3          .            .        
#> X7_1          .            .        
#> X7_2          .            .        
#> X7_3          .            .        
#> X8_1          0.07611936   0.2212063
#> X8_2         -0.01517658  -0.0426662
#> X8_3         -0.12663659  -0.3606695
#> X9_1          .            .        
#> X9_2          .            .        
#> X9_3          .            .        
#> X10_1         .            .        
#> X10_2         .            .        
#> X10_3         .            .        
#> X11_1         0.06458267   0.1329899
#> X11_2        -0.13771228  -0.3428515
#> X11_3        -0.26279204  -0.6303841
#> X12_1         .            .        
#> X12_2         .            .        
#> X12_3         .            .        
#> X13_1         .            .        
#> X13_2         .            .        
#> X13_3         .            .        
#> X14_1         .            .        
#> X14_2         .            .        
#> X14_3         .            .        
#> X15_1         .            .        
#> X15_2         .            .        
#> X15_3         .            .        
#> X16_1         .            .        
#> X16_2         .            .        
#> X16_3         .            .        
#> X17_1         .            .        
#> X17_2         .            .        
#> X17_3         .            .        
#> X18_1         .            .        
#> X18_2         .            .        
#> X18_3         .            .        
#> X19_1         .            .        
#> X19_2         .            .        
#> X19_3         .            .        
#> X20_1         .            .        
#> X20_2         .            .        
#> X20_3         .            .        
#> E             1.94035362   1.9703742
#> X1_1:E        .            .        
#> X1_2:E        .            .        
#> X1_3:E        .            .        
#> X2_1:E        .            .        
#> X2_2:E        .            .        
#> X2_3:E        .            .        
#> X3_1:E        0.89039027   1.4891105
#> X3_2:E       -0.75845463  -1.2853966
#> X3_3:E       -0.88087103  -1.2534744
#> X4_1:E       -0.61790227  -0.5802235
#> X4_2:E      -17.40450905 -17.6279480
#> X4_3:E       -3.72472712  -3.4668409
#> X5_1:E        .            .        
#> X5_2:E        .            .        
#> X5_3:E        .            .        
#> X6_1:E        .            .        
#> X6_2:E        .            .        
#> X6_3:E        .            .        
#> X7_1:E        .            .        
#> X7_2:E        .            .        
#> X7_3:E        .            .        
#> X8_1:E        .            .        
#> X8_2:E        .            .        
#> X8_3:E        .            .        
#> X9_1:E        .            .        
#> X9_2:E        .            .        
#> X9_3:E        .            .        
#> X10_1:E       .            .        
#> X10_2:E       .            .        
#> X10_3:E       .            .        
#> X11_1:E       .            .        
#> X11_2:E       .            .        
#> X11_3:E       .            .        
#> X12_1:E       .            .        
#> X12_2:E       .            .        
#> X12_3:E       .            .        
#> X13_1:E       .            .        
#> X13_2:E       .            .        
#> X13_3:E       .            .        
#> X14_1:E       .            .        
#> X14_2:E       .            .        
#> X14_3:E       .            .        
#> X15_1:E       .            .        
#> X15_2:E       .            .        
#> X15_3:E       .            .        
#> X16_1:E       .            .        
#> X16_2:E       .            .        
#> X16_3:E       .            .        
#> X17_1:E       .            .        
#> X17_2:E       .            .        
#> X17_3:E       .            .        
#> X18_1:E       .            .        
#> X18_2:E       .            .        
#> X18_3:E       .            .        
#> X19_1:E       .            .        
#> X19_2:E       .            .        
#> X19_3:E       .            .        
#> X20_1:E       .            .        
#> X20_2:E       .            .        
#> X20_3:E       .            .

Estimated non-zero coefficients at lambda.1se:

predict(cvfit, type = "nonzero")
#>                        1
#> (Intercept)   5.44728244
#> X1_1         -0.33479902
#> X1_2          0.46732277
#> X1_3          1.70401603
#> X3_1          2.12553380
#> X3_2         -1.81057790
#> X3_3         -2.10280952
#> X4_1         -0.26919665
#> X4_2         -7.58248628
#> X4_3         -1.62272272
#> X8_1          0.07611936
#> X8_2         -0.01517658
#> X8_3         -0.12663659
#> X11_1         0.06458267
#> X11_2        -0.13771228
#> X11_3        -0.26279204
#> E             1.94035362
#> X3_1:E        0.89039027
#> X3_2:E       -0.75845463
#> X3_3:E       -0.88087103
#> X4_1:E       -0.61790227
#> X4_2:E      -17.40450905
#> X4_3:E       -3.72472712

Visualizing the Effect of the Non-linear Terms

bsplines are difficult to interpret. We provide a plotting function to visualize the effect of the non-linear function on the response.

Main Effects

Since we are using simulated data, we also plot the true curve:

plotMain(cvfit$sail.fit, x = sailsim$x, xvar = "X3",
         legend.position = "topright",
         s = cvfit$lambda.min, f.truth = sailsim$f3)

Interaction Effects

Again, since we are using simulated data, we also plot the true interaction:

plotInter(cvfit$sail.fit, x = sailsim$x, xvar = "X4",
          f.truth = sailsim$f4.inter,
          s = cvfit$lambda.min,
          title_z = "Estimated")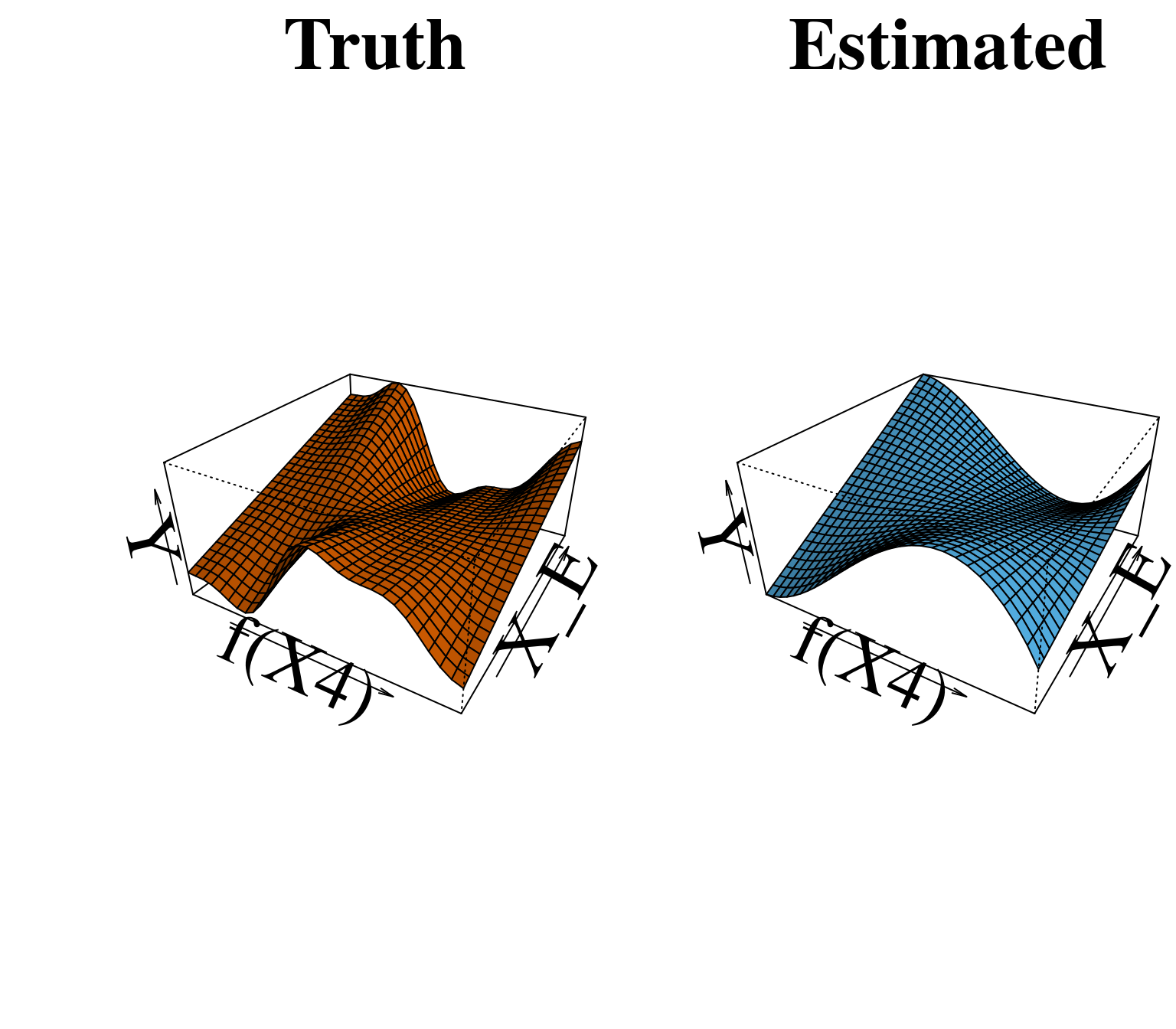

Linear Interactions

The basis argument in the sail function is very flexible in that it allows you to apply any basis expansion to the columns of \(\mathbf{X}\). Of course, there might be situations where you do not expect any non-linear main effects or interactions to be present in your data. You can still use the sail method to search for linear main effects and interactions. This can be accomplished by specifying an identity map:

f.identity <- function(i) i

We then pass this function to basis argument in cv.sail:

cvfit_linear <- cv.sail(x = sailsim$x, y = sailsim$y, e = sailsim$e,
                        basis = f.identity, nfolds = 5, parallel = TRUE,
                 dfmax = 10, # to speed up vignette build time
                        nlambda = 50)

Next we plot the cross-validated curve:

plot(cvfit_linear)

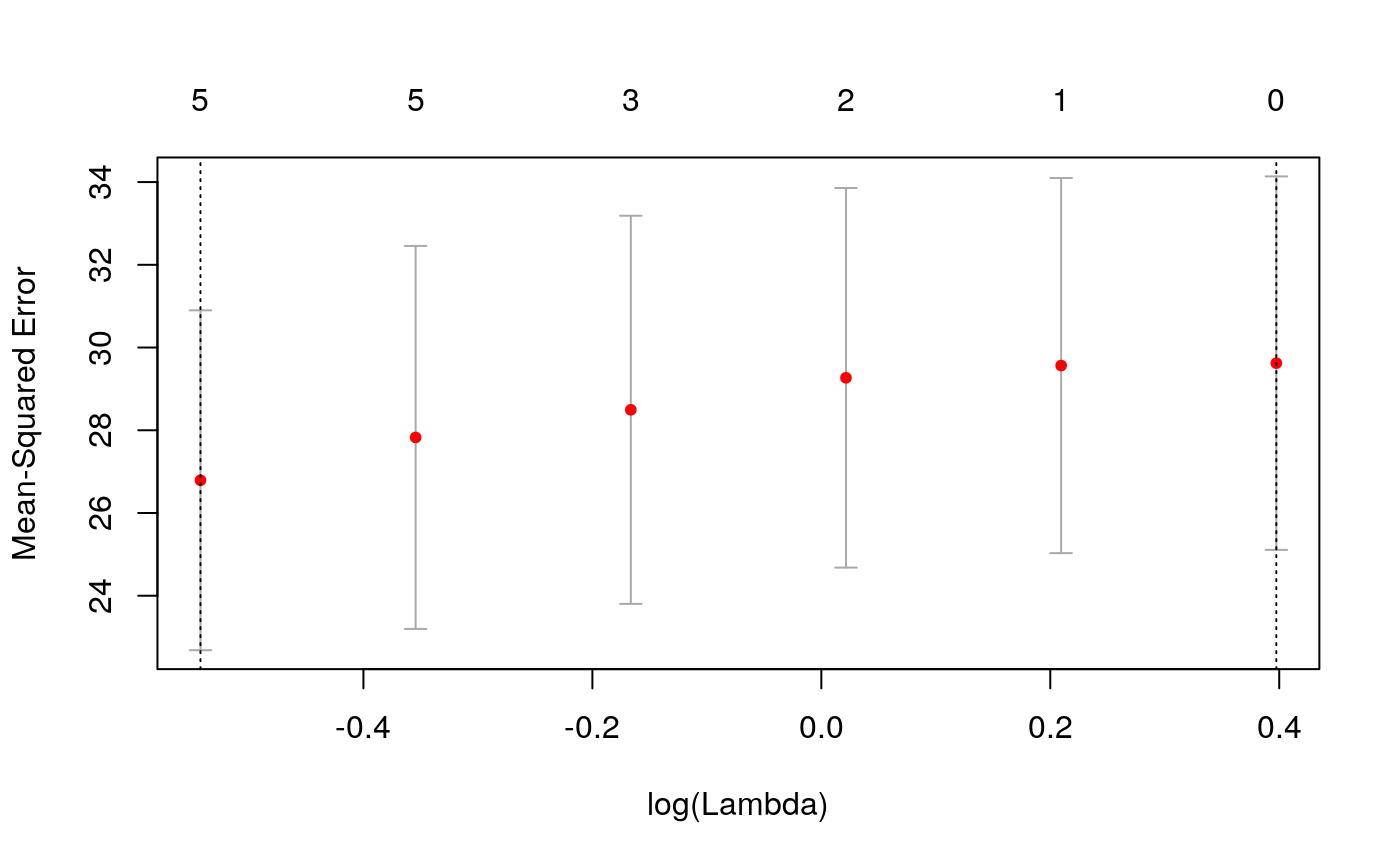
And extract the model at lambda.min:

coef(cvfit_linear, s = "lambda.min")
#> 42 x 1 sparse Matrix of class "dgCMatrix"
#>                      1
#> (Intercept)  5.2789845
#> X1_1         0.6445908
#> X2_1         .        
#> X3_1        -2.0254507
#> X4_1        -3.2233978
#> X5_1         .        
#> X6_1         .        
#> X7_1         .        
#> X8_1         .        
#> X9_1         .        
#> X10_1        .        
#> X11_1       -1.4226233
#> X12_1        .        
#> X13_1        .        
#> X14_1        .        
#> X15_1        .        
#> X16_1        .        
#> X17_1        .        
#> X18_1        .        
#> X19_1        .        
#> X20_1        .        
#> E            0.4723233
#> X1_1:E       .        
#> X2_1:E       .        
#> X3_1:E       .        
#> X4_1:E       .        
#> X5_1:E       .        
#> X6_1:E       .        
#> X7_1:E       .        
#> X8_1:E       .        
#> X9_1:E       .        
#> X10_1:E      .        
#> X11_1:E      .        
#> X12_1:E      .        
#> X13_1:E      .        
#> X14_1:E      .        
#> X15_1:E      .        
#> X16_1:E      .        
#> X17_1:E      .        
#> X18_1:E      .        
#> X19_1:E      .        
#> X20_1:E      .

Applying a different penalty to each predictor

Recall that we consider the following penalized least squares criterion for this problem:

\[\begin{equation} \arg\min_{\boldsymbol{\theta} } \mathcal{L}(Y;\boldsymbol{\theta}) + \lambda (1-\alpha) \left( w_E |\beta_E| + \sum_{j=1}^{p} w_j \lVert\boldsymbol{\theta}_j \rVert_2 \right) + \lambda\alpha \sum_{j=1}^{p} w_{jE} |\gamma_{j}| \end{equation}\]

The weights \(w_E, w_j, w_{jE}\) are by default set to 1 as specified by the penalty.factor argument. This argument allows users to apply separate penalty factors to each coefficient. In particular, any variable with penalty.factor equal to zero is not penalized at all. This feature can be applied mainly for two reasons:

Prior knowledge about the importance of certain variables is known. Larger weights will penalize the variable more, while smaller weights will penalize the variable less
Allows users to apply the Adaptive sail, similar to the Adaptive Lasso

In the following example, we want the environment variable to always be included so we set the first element of p.fac to zero. We also want to apply less of a penalty to the main effects for \(X_2, X_3, X_4\):

# the weights correspond to E, X1, X2, X3, ... X_p, X1:E, X2:E, ... X_p:E
p.fac <- c(0, 1, 0.4, 0.6, 0.7, rep(1, 2*ncol(sailsim$x) - 4))

fit_pf <- sail(x = sailsim$x, y = sailsim$y, e = sailsim$e, basis = f.basis,
               nlambda = 50,
               dfmax = 10, # to speed up vignette build time
               penalty.factor = p.fac)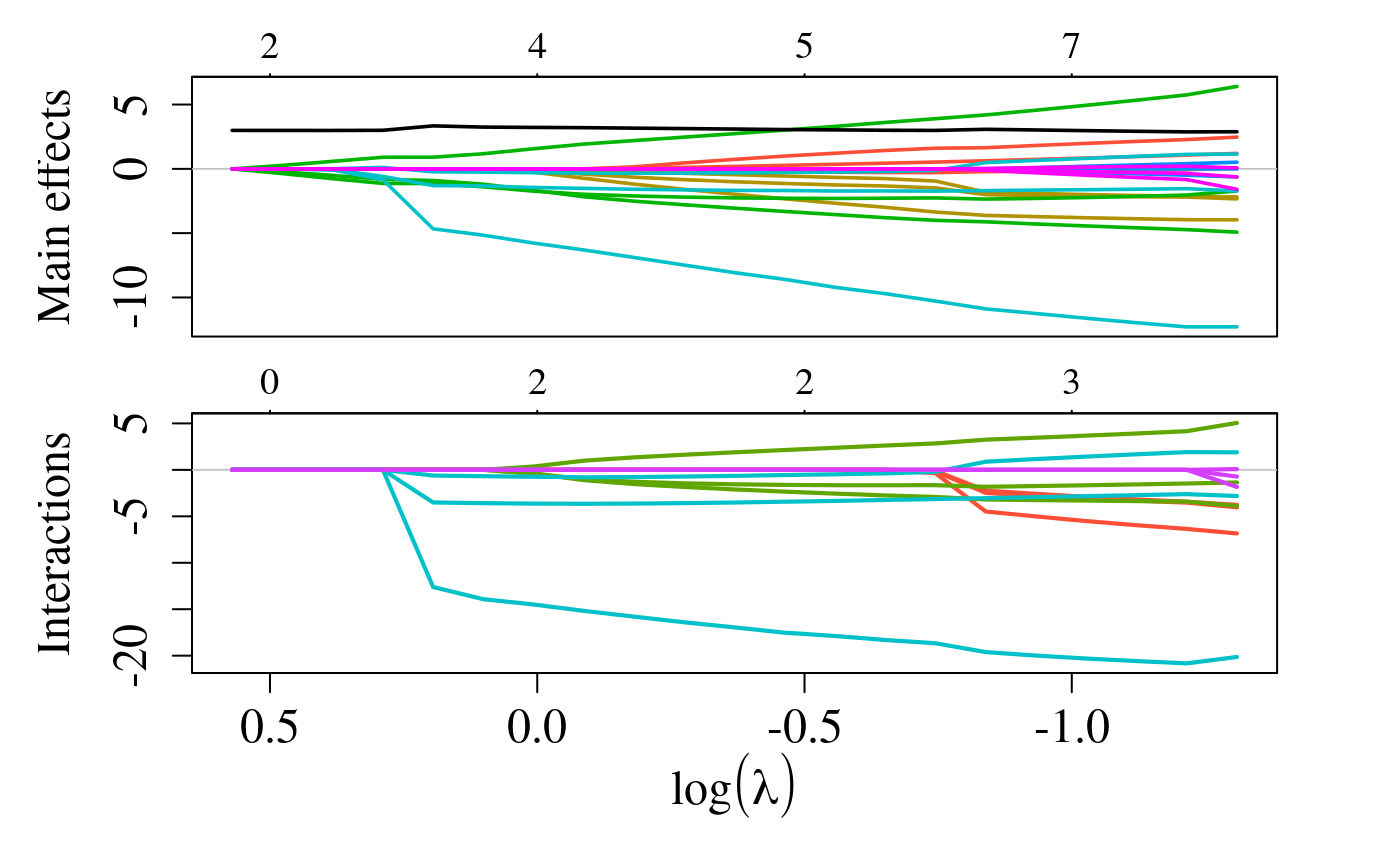

plot(fit_pf)

We see from the plot above that the black line (corresponding to the \(E\) variable with penalty.factor equal to zero) is always included in the model.

Sahir Rai Bhatnagar

2019-11-19