Causal Inference

In the precision medicine paradigm, treatment decisions are tailored to individuals rather than relying on a ‘one-size-fits-all’ approach. This approach to treatment is beneficial when treatment effects are heterogeneous. For example, effective management of stress requires the development of personalised approaches, as patients with different characteristics respond to and engage with treatments differently. With the aim of improving individuals’ health outcomes, individualised treatment rules (ITRs) recommend effective treatments based on each person’s specific characteristics. However, collected data often contain many variables that are irrelevant for tailoring treatment. Including all variables in an analysis could reduce statistical efficiency by estimating unnecessary coefficients whose estimates fluctuate around zero for variables that are not useful for tailoring treatment, and yielding an unnecessarily complicated treatment decision rule that is difficult for physicians to interpret or implement. It is therefore important to develop variable selection methods with the objective of optimising individuals’ outcomes by identifying useful tailoring variables.

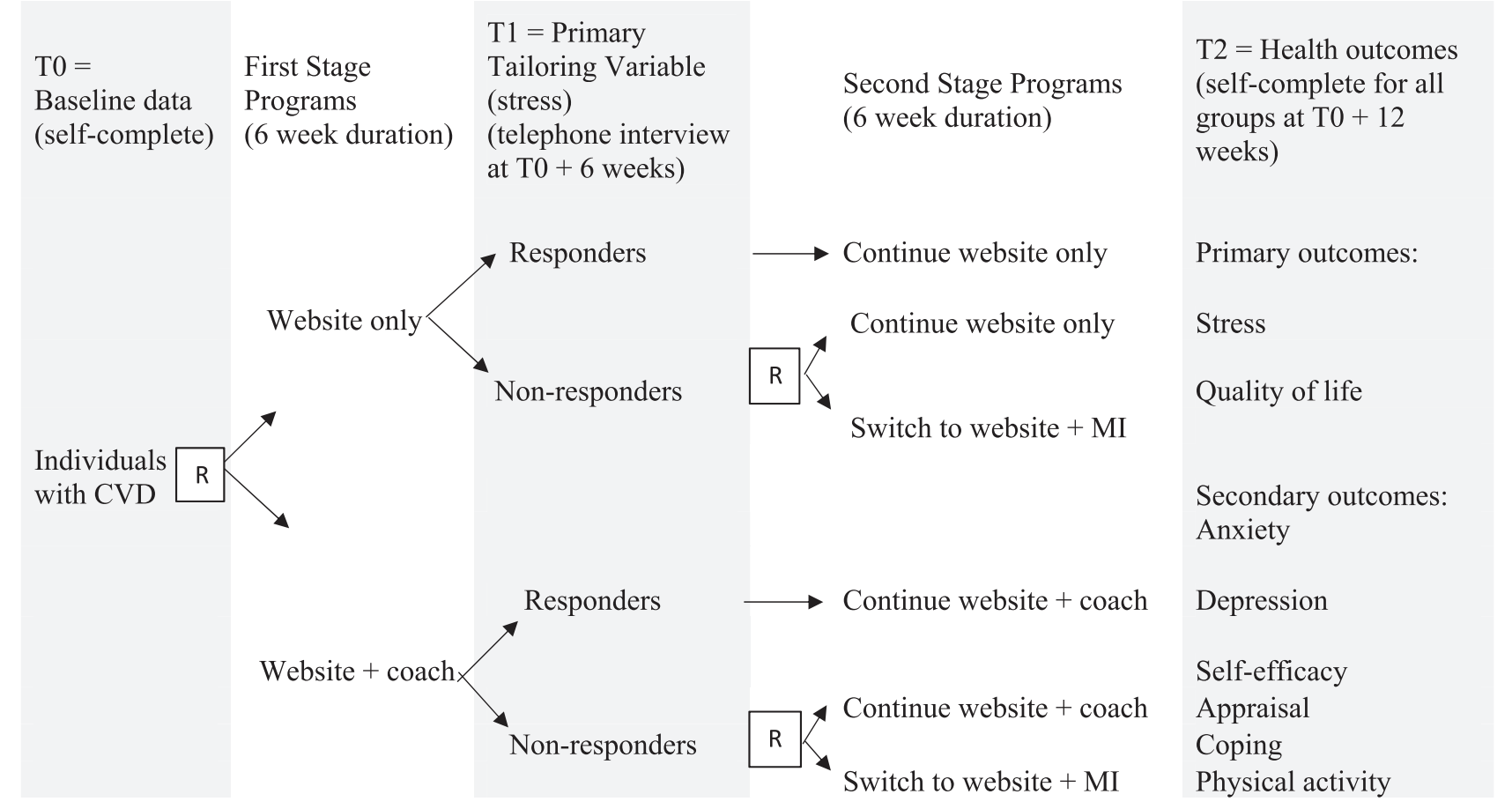
We are motivated by a Sequential Multiple Assignment Randomization Trial (SMART) design to optimize the delivery of a web-based, stress management intervention for patients with a cardiovascular disease (CVD). The trial aimed to assess an intervention adapted across time using a stepped-care approach where patients who do not respond to the initial intervention are re-randomized to receive an alternative intervention (Figure 1). A goal of ITR analysis in this setting is to identify the optimal treatment rule that assigns patients to the most effective treatment based on their individual characteristics.

Building on previous work of variable selection for interaction selection (Bhatnagar et al., 2023), my PhD student Zeyu Bian (co-supervised by Dr. Erica Moodie), developed an ITR method using penalized dynamic weighted least squares (Bian et al., 2021; Bian et al., 2023). Our method has the strong heredity property, that is, an interaction term can be included in the model only if the corresponding main terms have also been selected. We show our method has both the double robustness property and the oracle property theoretically. We then extended this framework to count and binary outcome data and applied it to the SMART trial (Bian et al., 2024). The primary outcome in this analysis was the stress subscale from the Depression Anxiety Stress Scales (DASS), which is a count outcome measured at 6 weeks after stage 1 randomised allocation. A lower DASS-stress subscale score suggests the presence of fewer symptoms of stress, so the optimal treatment decision minimises the DASS-stress subscale score. We found that five variables were relevant for tailoring treatment: DASS at baseline, sex, marital status, stomach condition, and vision. The estimated treatment rule is

For example, a married woman who does not have either a vision problem or a stomach ailment and who has a DASS greater than 13 would be recommended for website plus weekly telephone coaching.