10 The Sampling Distribution

10.1 Student Learning Objective

In this section we integrate the concept of data that is extracted from a sample with the concept of a random variable. The new element that connects between these two concepts is the notion of sampling distribution. The data we observe results from the specific sample that was selected. The sampling distribution, in a similar way to random variables, corresponds to all samples that could have been selected. (Or, stated in a different tense, to the sample that will be selected prior to the selection itself.) Summaries of the distribution of the data, such as the sample mean and the sample standard deviation, become random variables when considered in the context of the sampling distribution. In this section we investigate the sampling distribution of such data summaries. In particular, it is demonstrated that (for large samples) the sampling distribution of the sample average may be approximated by the Normal distribution. The mathematical theorem that proves this approximation is called the Central Limit Theory. By the end of this chapter, the student should be able to:

Comprehend the notion of sampling distribution and simulate the sampling distribution of the sample average.
Relate the expectation and standard deviation of a measurement to the expectation and standard deviation of the sample average.
Apply the Central Limit Theorem to the sample averages.

10.2 The Sampling Distribution

In Chapter 7 the concept of a random variable was introduced. As part of the introduction we used an example that involved the selection of a random person from the population and the measuring of his/her height. Prior to the action of selection, the height of that person is a random variable. It has the potential of obtaining any of the heights that are present in the population, which is the sample space of this example, with a distribution that reflects the relative frequencies of each of the heights in the population: the probabilities of the values. After the selection of the person and the measuring of the height we get a particular value. This is the observed value and is no longer a random variable. In this section we extend the concept of a random variable and define the concept of a random sample.

10.2.1 A Random Sample

The relation between the random sample and the data is similar to the relation between a random variable and the observed value. The data is the observed values of a sample taken from a population. The content of the data is known. The random sample, similarly to a random variable, is the data that will be selected when taking a sample, prior to the selection itself. The content of the random sample is unknown, since the sample has not yet been taken. Still, just like for the case of the random variable, one is able to say what the possible evaluations of the sample may be and, depending on the mechanism of selecting the sample, what are the probabilities of the different potential evaluations. The collection of all possible evaluations of the sample is the sample space of the random sample and the probabilities of the different evaluations produce the distribution of the random sample.

(Alternatively, if one prefers to speak in past tense, one can define the sample space of a random sample to be the evaluations of the sample that could have taken place, with the distribution of the random sample being the probabilities of these evaluations.)

A statistic is a function of the data. Example of statistics are the average of the data, the sample variance and standard deviation, the median of the data, etc. In each case a given formula is applied to the data. In each type of statistic a different formula is applied.

The same formula that is applied to the observed data may, in principle, be applied to random samples. Hence, for example, one may talk of the sample average, which is the average of the elements in the data. The average, considered in the context of the observed data, is a number and its value is known. However, if we think of the average in the context of a random sample then it becomes a random variable. Prior to the selection of the actual sample we do not know what values it will include. Hence, we cannot tell what the outcome of the average of the values will be. However, due to the identification of all possible evaluations that the sample can possess we may say in advance what is the collection of values the sample average can have. This is the sample space of the sample average. Moreover, from the sampling distribution of the random sample one may identify the probability of each value of the sample average, thus obtaining the sampling distribution of the sample average.

The same line of argumentation applies to any statistic. Computed in the context of the observed data, the statistic is a known number that may, for example, be used to characterize the variation in the data. When thinking of a statistic in the context of a random sample it becomes a random variable. The distribution of the statistic is called the sampling distribution of the statistic. Consequently, we may talk of the sampling distribution of the median, the sample distribution of the sample variance, etc.

Random variables are also applied as models for uncertainty in future measurements in more abstract settings that need not involve a specific population. Specifically, we introduced the Binomial and Poisson random variables for settings that involve counting and the Uniform, Exponential, and Normal random variables for settings where the measurement is continuous.

The notion of a sampling distribution may be extended to a situation where one is taking several measurements, each measurement taken independently of the others. As a result one obtains a sequence of measurements. We use the term “sample” to denote this sequence. The distribution of this sequence is also called the sampling distribution. If all the measurements in the sequence are Binomial then we call it a Binomial sample. If all the measurements are Exponential we call it an Exponential sample and so forth.

Again, one may apply a formula (such as the average) to the content of the random sequence and produce a random variable. The term sampling distribution describes again the distribution that the random variable produced by the formula inherits from the sample.

In the next subsection we examine an example of a sample taken from a population. Subsequently, we discuss examples that involves a sequence of measurements from a theoretical model.

10.2.2 Sampling From a Population

Consider taking a sample from a population. Let us use again for the illustration the heights_population.csv file that contains the population data and can be obtained here like we did in Chapter 7. The data frame produced from the file contains the sex and hight of the 100,000 members of some imaginary population. Recall that in Chapter 7 we applied the function sample to randomly sample the height of a single subject from the population. Let us apply the same function again, but this time in order to sample the heights of 100 subjects:

heights_population <- rio::import(here::here("inst/data/heights_population.csv"))
heights_population <- heights_population %>% 
  dplyr::mutate(sex = factor(sex))
Y.samp <- heights_population %>%
  dplyr::slice_sample(n = 100, replace = FALSE)
Y.samp %>% 
  dplyr::glimpse()
#> Rows: 100
#> Columns: 3
#> $ id     <int> 3776094, 8205435, 2010906, 6929553, 9381841…
#> $ sex    <fct> MALE, MALE, FEMALE, FEMALE, MALE, FEMALE, F…
#> $ height <int> 177, 173, 163, 167, 174, 163, 160, 150, 167…

Typically, a researcher does not get to examine the entire population. Instead, measurements on a sample from the population are made. In relation to the imaginary setting we simulate in the example, the typical situation is that the research does not have the complete list of potential measurement evaluations, i.e. the complete list of 100,000 heights, but only a sample of measurements, namely the list of 100 rows that are stored in Y.samp and are presented above. The role of statistics is to make inference on the parameters of the unobserved population based on the information that is obtained from the sample.

For example, we may be interested in estimating the mean value of the heights in the population. A reasonable proposal is to use the sample average to serve as an estimate:

mean(Y.samp$height)
#> [1] 168.32

In our artificial example we can actually compute the true population mean:

mean(heights_population$height)
#> [1] 170.035

Hence, we may see that although the match between the estimated value and the actual value is not perfect still they are close enough.

The actual estimate that we have obtained resulted from the specific sample that was collected. Had we collected a different subset of 100 individuals we would have obtained different numerical value for the estimate. Consequently, one may wonder: Was it pure luck that we got such good estimates? How likely is it to get estimates that are close to the target parameter?

Notice that in realistic settings we do not know the actual value of the target population parameters. Nonetheless, we would still want to have at least a probabilistic assessment of the distance between our estimates and the parameters they try to estimate. The sampling distribution is the vehicle that may enable us to address these questions.

In order to illustrate the concept of the sampling distribution let us select another sample and compute its average:

Y.samp <- heights_population %>%
  dplyr::slice_sample(n = 100, replace = FALSE)

and do it once more:

Y.samp <- heights_population %>%
  dplyr::slice_sample(n = 100, replace = FALSE)
mean(Y.samp$height)
#> [1] 171.04

In each case we got a different value for the sample average. In the first of the last two iterations the result was more than 1 centimeter away from the population average, which is equal to 170.035, and in the second it was within the range of 1 centimeter. Can we say, prior to taking the sample, what is the probability of falling within 1 centimeter of the population mean?

Chapter 7 discussed the random variable that emerges by randomly sampling a single number from the population presented by the sequence heights_population$height. The distribution of the random variable resulted from the assignment of the probability 1/100,000 to each one of the 100,000 possible outcomes. The same principle applies when we randomly sample 100 individuals. Each possible outcome is a collection of 100 numbers and each collection is assigned equal probability. The resulting distribution is called the sampling distribution.

The distribution of the average of the sample emerges from this distribution: With each sample one may associate the average of that sample. The probability assigned to that average outcome is the probability of the sample. Hence, one may assess the probability of falling within 1 centimeter of the population mean using the sampling distribution. Each sample produces an average that either falls within the given range or not. The probability of the sample average falling within the given range is the proportion of samples for which this event happens among the entire collection of samples.

However, we face a technical difficulty when we attempt to assess the sampling distribution of the average and the probability of falling within 1 centimeter of the population mean. Examination of the distribution of a sample of a single individual is easy enough. The total number of outcomes, which is 100,000 in the given example, can be handled with no effort by the computer. However, when we consider samples of size 100 we get that the total number of ways to select 100 number out of 100,000 numbers is in the order of $10^{342}$ (1 followed by 342 zeros) and cannot be handled by any computer. Thus, the probability cannot be computed.

As a compromise we will approximate the distribution by selecting a large number of samples, say 100,000, to represent the entire collection, and use the resulting distribution as an approximation of the sampling distribution. Indeed, the larger the number of samples that we create the more accurate the approximation of the distribution is. Still, taking 100,000 repeats should produce approximations which are good enough for our purposes.

Consider the sampling distribution of the sample average. We simulated above a few examples of the average. Now we would like to simulate 100,000 such examples. We do this by creating first a sequence of the length of the number of evaluations we seek (100,000) and then write a small program that produces each time a new random sample of size 100 and assigns the value of the average of that sample to the appropriate position in the sequence. Do first and explain later⁶⁴:

Y.bar <- rep(0,10^5)
for(i in 1:10^5) {
  Y.samp <- sample(heights_population$height,100)
  Y.bar[i] <- mean(Y.samp)
}

In the first line we produce a sequence of length 100,000 that contains zeros. The function “rep” creates a sequence that contains repeats of its first argument a number of times that is specified by its second argument. In this example, the numerical value 0 is repeated 100,000 times to produce a sequence of zeros of the length we seek.

The main part of the program is a “for” loop. The argument of the function “for” takes the special form: “index.name in index.values”, where index.name is the name of the running index and index.values is the collection of values over which the running index is evaluated. In each iteration of the loop the running index is assigned a value from the collection and the expression that follows the brackets of the “for” function is evaluated with the given value of the running index.

In the given example the collection of values is produced by the expression “1:n”. Recall that the expression “1:n” produces the collection of integers between 1 and n. Here, n = 100,000. Hence, in the given application the collection of values is a sequence that contains the integers between 1 and 100,000. The running index is called “i”. the expression is evaluated 100,000 times, each time with a different integer value for the running index “i”.

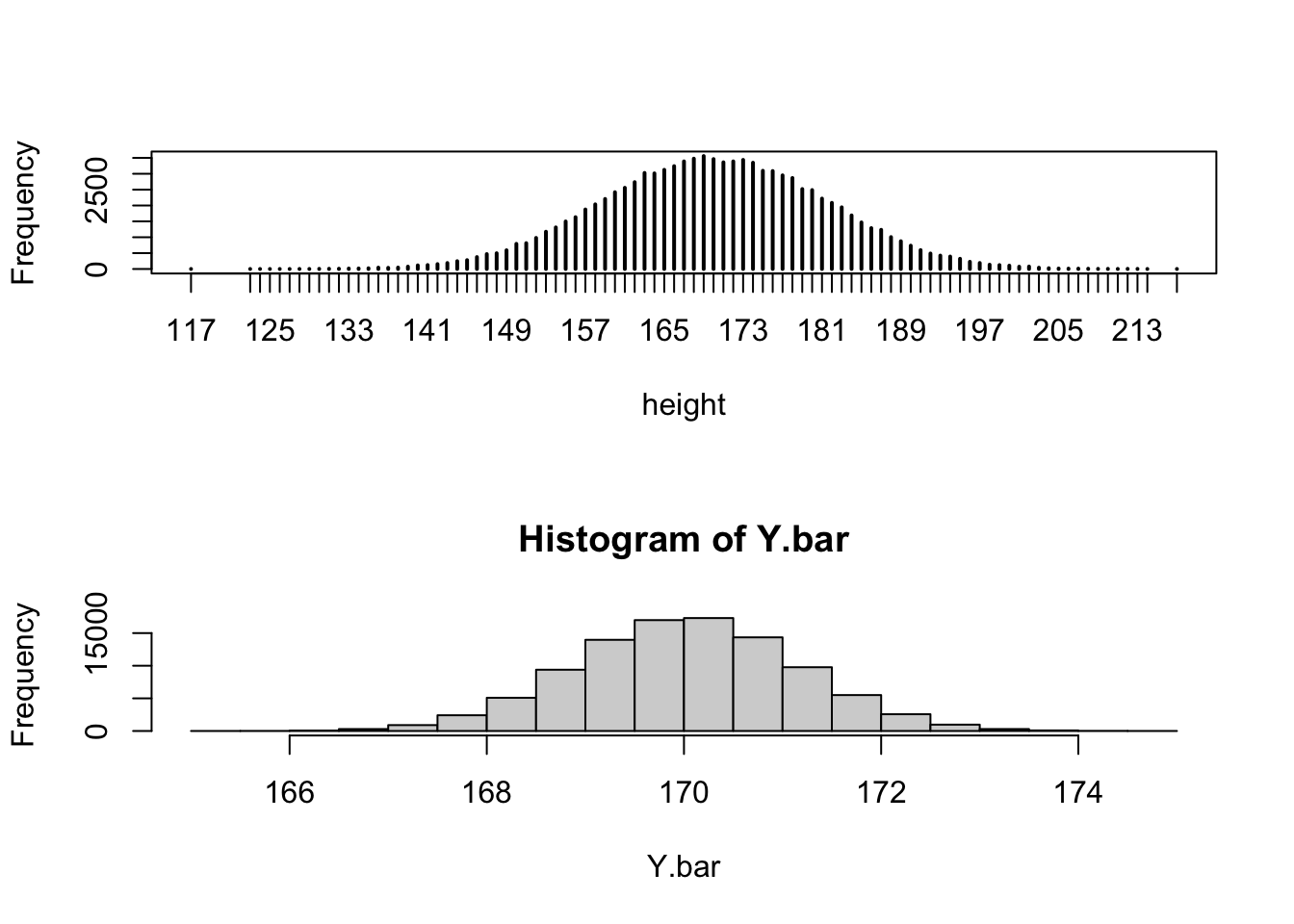
Figure 10.1: Distribution of Height and the Sampling Distribution of Averages

The R system treats a collection of expressions enclosed within curly brackets as one entity. Therefore, in each iteration of the “for” loop, the lines that are within the curly brackets are evaluated. In the first line a random sample of size 100 is produced and in the second line the average of the sample is computed and stored in the $i$-th position of the sequence “Y.bar”. Observe that the specific position in the sequence is referred to by using square brackets.

The program changes the original components of the sequence, from 0 to the average of a random sample, one by one. When the loop ends all values are changed and the sequence “Y.bar” contains 100,000 evaluations of the sample average. The last line, which is outside the curly brackets and is evaluated after the “for” loop ends, produces an histogram of the averages that were simulated. The histogram is presented in the lower panel of Figure 10.1.

Compare the distribution of the sample average to the distribution of the heights in the population that was presented first in Figure 7.2 and is currently presented in the upper panel of Figure 10.1. Observe that both distributions are centered at about 170 centimeters. Notice, however, that the range of values of the sample average lies essentially between 166 and 174 centimeters, whereas the range of the distribution of heights themselves is between 127 and 217 centimeter. Broadly speaking, the sample average and the original measurement are centered around the same location but the sample average is less spread.

Specifically, let us compare the expectation and standard deviation of the sample average to the expectation and standard deviation of the original measurement:

mean(heights_population$height)
#> [1] 170.035
sd(heights_population$height)
#> [1] 11.23205
mean(Y.bar)
#> [1] 170.0276
sd(Y.bar)
#> [1] 1.125938

Observe that the expectation of the population and the expectation of the sample average, are practically the same, the standard deviation of the sample average is about 10 times smaller than the standard deviation of the population. This result is not accidental and actually reflects a general phenomena that will be seen below in other examples.

We may use the simulated sampling distribution in order to compute an approximation of the probability of the sample average falling within 1 centimeter of the population mean. Let us first compute the relevant probability and then explain the details of the computation:

mean(abs(Y.bar - mean(heights_population$height)) <= 1)
#> [1] 0.62556

Hence we get that the probability of the given event is about 62.6%.

The object “Y.bar” is a sequence of length 100,000 that contains the simulated sample averages. This sequence represents the distribution of the sample average. The expression “abs(Y.bar - mean(heights_population$height)) <= 1” produces a sequence of logical “TRUE” or “FALSE” values, depending on the value of the sample average being less or more than one unit away from the population mean. The application of the function “mean” to the output of the last expression results in the computation of the relative frequency of TRUEs, which corresponds to the probability of the event of interest.

Example 10.1 Consider a poll for the determination of the support in the population for a candidate. The proportion in the population of supporters was denoted by $p$. A sample of size $n=300$ was considered in order to estimate the size of $p$. We identified that the distribution of $X$, the number of supporters in the sample, is $\mathrm{Binomial}(300,p)$. This distribution is the sampling distribution⁶⁵ of $Y$. One may use the proportion in the sample of supporters, the number of supporters in the sample divided by 300, as an estimate to the parameter $p$. The sampling distribution of this quantity, $Y/300$, may be considered in order to assess the discrepancy between the estimate and the actual value of the parameter.

10.2.3 Theoretical Models

Sampling distribution can also be considered in the context of theoretical distribution models. For example, take a measurement $Y \sim \mathrm{Binomial}(10,0.5)$ from the Binomial distribution. Assume 64 independent measurements are produced with this distribution: $Y_1, Y_2, \ldots, Y_{64}$. The sample average in this case corresponds to the distribution of the random variable produced by averaging these 64 random variables:

\[\bar Y = \frac{Y_1 + Y_2 + \cdots + Y_{64}} {64} = \frac{1}{64}\sum_{i=1}^{64} Y_i\;.\] Again, one may wonder what is the distribution of the sample average $\bar Y$ in this case?

We can approximate the distribution of the sample average by simulation. The function “rbinom” produces a random sample from the Binomial distribution. The first argument to the function is the sample size, which we take in this example to be equal to 64. The second and third arguments are the parameters of the Binomial distribution, 10 and 0.5 in this case. We can use this function in the simulation:

Y.bar <- rep(0,10^5)
for(i in 1:10^5) {
  Y.samp <- rbinom(64,10,0.5)
  Y.bar[i] <- mean(Y.samp)
}

Observe that in this code we created a sequence of length 100,000 with evaluations of the sample average of 64 Binomial random variables. We start with a sequence of zeros and in each iteration of the “for” loop a zero is replaced by the average of a random sample of 64 Binomial random variables.

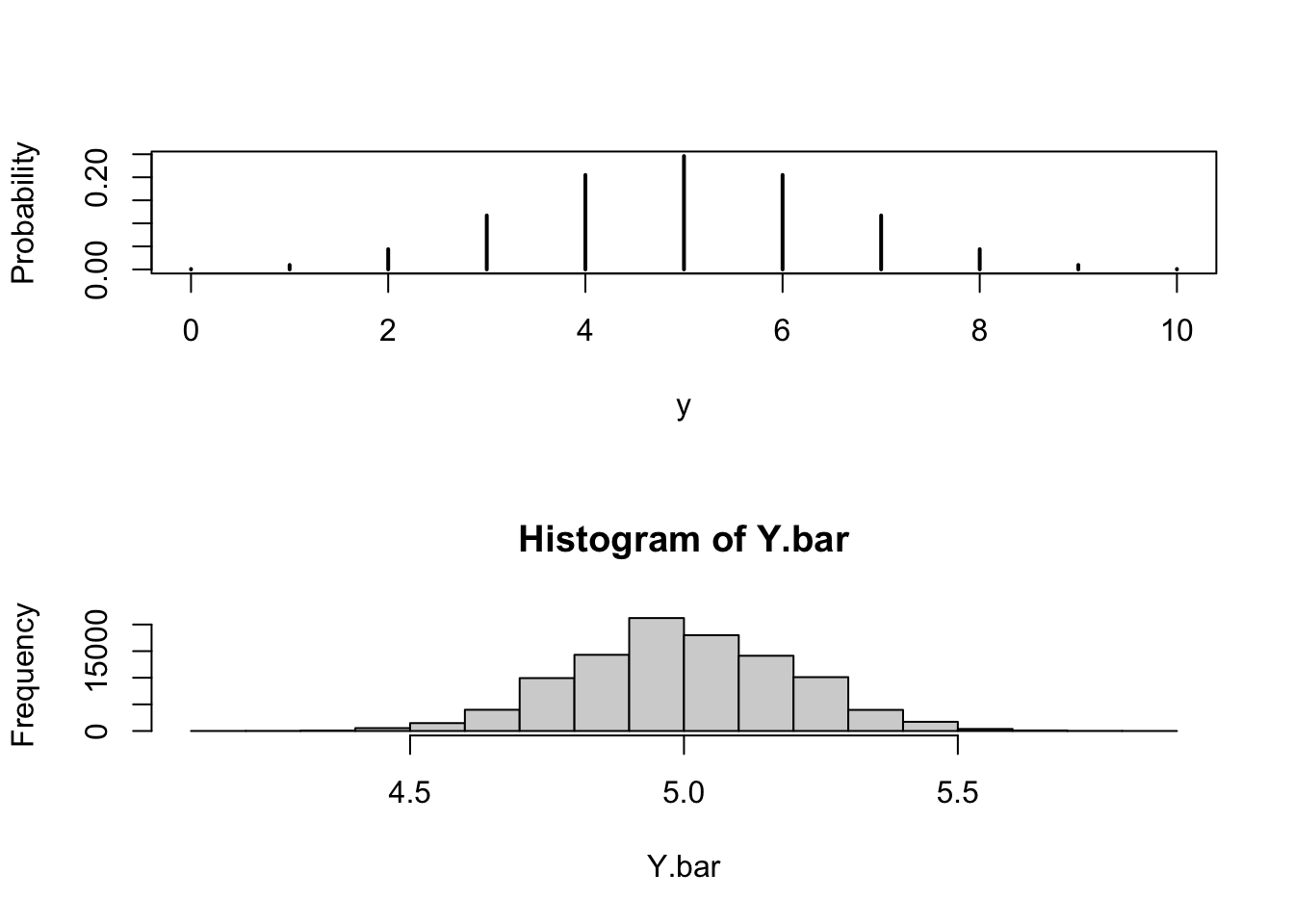
Figure 10.2: Distributions of an Average and a Single Binomial(10,0.5)

Examine the sampling distribution of the Binomial average:

mean(Y.bar)
#> [1] 5.000628
sd(Y.bar)
#> [1] 0.1976092

The histogram of the sample average is presented in the lower panel of Figure 10.2. Compare it to the distribution of a single Binomial random variable that appears in the upper panel. Notice, once more, that the center of the two distributions coincide but the spread of the sample average is smaller. The sample space of a single Binomial random variable is composed of integers. The sample space of the average of 64 Binomial random variables, on the other hand, contains many more values and is closer to the sample space of a random variable with a continuous distribution.

Recall that the expectation of a $\mathrm{Binomial}(10,0.5)$ random variable is $\operatorname{E}(Y) = 10 \cdot 0.5 = 5$ and the variance is $\operatorname{Var}(Y) = 10 \cdot 0.5 \cdot 0.5 = 2.5$ (thus, the standard deviation is $\sqrt{2.5} = 1.581139$). Observe that the expectation of the sample average that we got from the simulation is essentially equal to 5 and the standard deviation is 0.1982219.

In Section 8, we proved mathematically that the expectation of the sample mean is equal to the theoretical expectation of its components:

\[\operatorname{E}(\bar Y) = \operatorname{E}(Y)\;.\] The results of the simulation for the expectation of the sample average are consistent with the mathematical statement. In Section 8, we also proved that the variance of the sample average is equal to the variance of each of the components, divided by the sample size:

\[\operatorname{Var}(\bar Y) = \operatorname{Var}(Y)/n\;,\] here $n$ is the number of observations in the sample. Specifically, in the Binomial example we get that $\operatorname{Var}(\bar Y) = 2.5/64$, since the variance of a Binomial component is 2.5 and there are 64 observations. Consequently, the standard deviation is $\sqrt{2.5/64} = 0.1976424$, in agreement, more or less, with the results of the simulation (that produced 0.1982219 as the standard deviation).

Consider the problem of identifying the central interval that contains 95% of the distribution. In the Normal distribution we were able to use the function “qnorm” in order to compute the percentiles of the theoretical distribution. A function that can be used for the same purpose for simulated distribution is the function “quantile”. The first argument to this function is the sequence of simulated values of the statistic, “Y.bar” in the current case. The second argument is a number between 0 and 1, or a sequence of such numbers:

quantile(x = Y.bar, probs = c(0.025,0.975))
#>     2.5%    97.5% 
#> 4.609375 5.390625

We used the sequence “c(0.025,0.975)” as the input to the second argument. As a result we obtained the output 4.609375, which is the 2.5%-percentile of the sampling distribution of the average, and 5.390625, which is the 97.5%-percentile of the sampling distribution of the average.

Of interest is to compare these percentiles to the parallel percentiles of the Normal distribution with the same expectation and the same standard deviation as the average of the Binomials:

qnorm(c(0.025,0.975),mean(Y.bar),sd(Y.bar))
#> [1] 4.613321 5.387935

Observe the similarity between the percentiles of the distribution of the average and the percentiles of the Normal distribution. This similarity is a reflection of the Normal approximation of the sampling distribution of the average, which is formulated in the next section under the title: The Central Limit Theorem.

Example 10.2 The distribution of the number of events of radio active decay in a second can be modeled according to the Poisson distribution. A quantity of interest is $\lambda$, the expectation of that Poisson distribution. This quantity may be estimated by measuring the total number of decays over a period of time and dividing the outcome by the number of seconds in that period of time. Let $n$ be this number of second. The procedure just described corresponds to taking the sample average of $\mathrm{Poisson}(\lambda)$ observations for a sample of size $n$. The expectation of the sample average is $\lambda$ and the variance is $\lambda/n$, leading to a standard deviation of size $\sqrt{\lambda/n}$. The Central Limit Theorem states that the sampling distribution of this average corresponds, approximately, to the Normal distribution with this expectation and standard deviation.

10.3 Law of Large Numbers and Central Limit Theorem

The Law of Large Numbers and the Central Limit Theorem are mathematical theorems that describe the sampling distribution of the average for large samples.

10.3.1 The Law of Large Numbers

The Law of Large Numbers states that, as the sample size becomes larger, the sampling distribution of the sample average becomes more and more concentrated about the expectation.

Let us demonstrate the Law of Large Numbers in the context of the Uniform distribution. Let the distribution of the measurement $Y$ be $\mathrm{Uniform}(3,7)$. Consider three different sample sizes $n$: $n=10$, $n=100$, and $n=1000$. Let us carry out a simulation similar to the simulations of the previous section. However, this time we run the simulation for the three sample sizes in parallel:

unif.10 <- rep(0,10^5)
unif.100 <- rep(0,10^5)
unif.1000 <- rep(0,10^5)
for(i in 1:10^5) {
  Y.samp.10 <- runif(10,3,7)
  unif.10[i] <- mean(Y.samp.10)
  Y.samp.100 <- runif(100,3,7)
  unif.100[i] <- mean(Y.samp.100)
  Y.samp.1000 <- runif(1000,3,7)
  unif.1000[i] <- mean(Y.samp.1000)
}

Observe that we have produced 3 sequences of length 100,000 each: “unif.10”, “unif.100”, and “unif.1000”. The first sequence is an approximation of the sampling distribution of an average of 10 independent Uniform measurements, the second approximates the sampling distribution of an average of 100 measurements and the third the distribution of an average of 1000 measurements. The distribution of single measurement in each of the examples is $\mathrm{Uniform}(3,7)$.

Consider the expectation of sample average for the three sample sizes:

mean(unif.10)
#> [1] 4.999444
mean(unif.100)
#> [1] 5.000308
mean(unif.1000)
#> [1] 5.000169

For all sample size the expectation of the sample average is equal to 5, which is the expectation of the $\mathrm{Uniform}(3,7)$ distribution.

Recall that the variance of the $\mathrm{Uniform}(a,b)$ distribution is $(b-a)^2/12$. Hence, the variance of the given Uniform distribution is $\operatorname{Var}(X) = (7-3)^2/12 = 16/12 \approx 1.3333$. The variances of the sample averages are:

var(unif.10)
#> [1] 0.1332605
var(unif.100)
#> [1] 0.01330791
var(unif.1000)
#> [1] 0.001339139

Notice that the variances decrease with the increase of the sample sizes. The decrease is according to the formula $\operatorname{Var}(\bar Y) = \operatorname{Var}(Y)/n$.

The variance is a measure of the spread of the distribution about the expectation. The smaller the variance the more concentrated is the distribution around the expectation. Consequently, in agreement with the Law of Large Numbers, the larger the sample size the more concentrated is the sampling distribution of the sample average about the expectation.

10.3.2 The Central Limit Theorem (CLT)

The Law of Large Numbers states that the distribution of the sample average tends to be more concentrated as the sample size increases. The Central Limit Theorem (CLT in short) provides an approximation of this distribution.

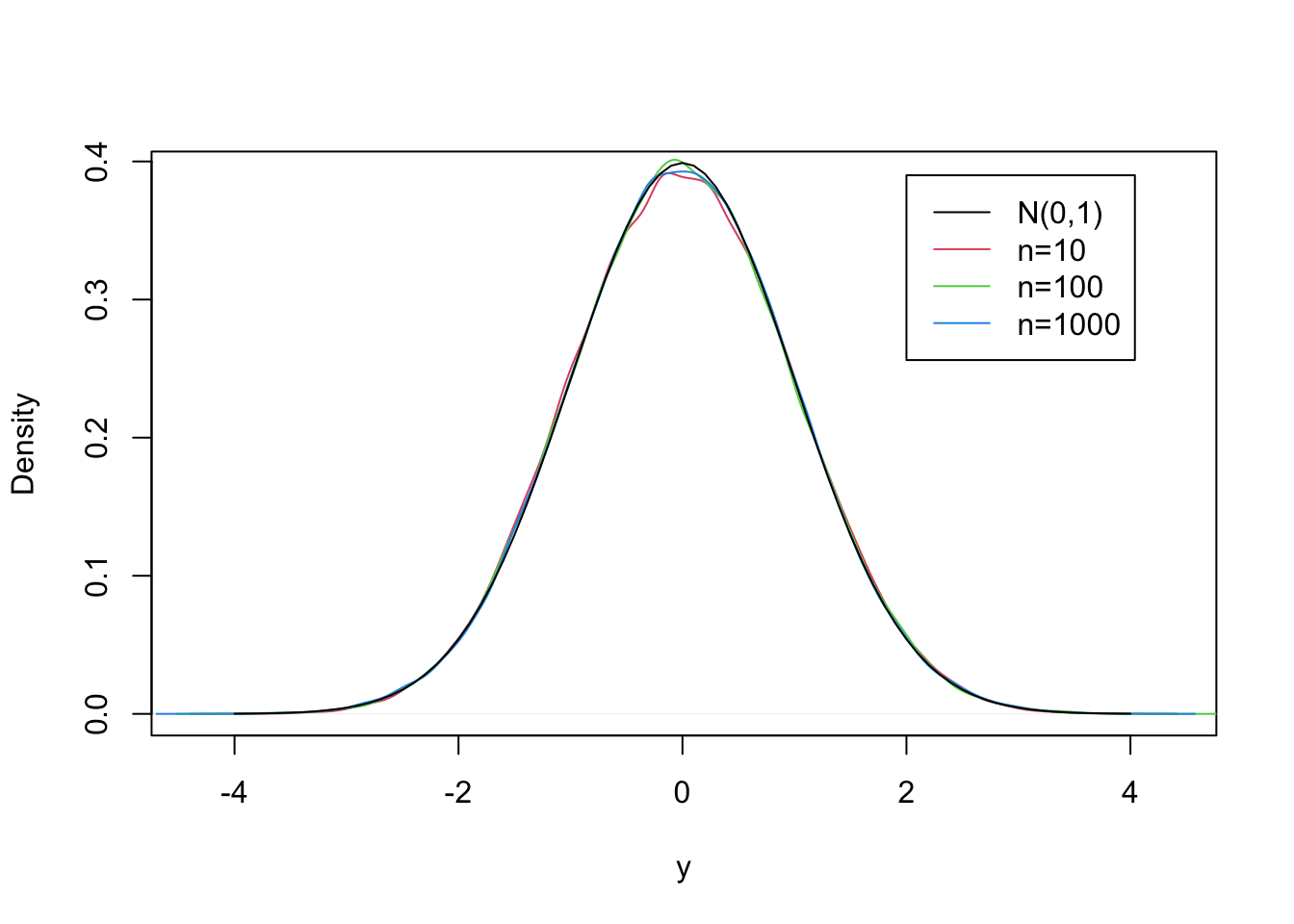
Figure 10.3: The CLT for the Uniform(3,7) Distribution

The deviation between the sample average and the expectation of the measurement tend to decreases with the increase in sample size. In order to obtain a refined assessment of this deviation one needs to magnify it. The appropriate way to obtain the magnification is to consider the standardized sample average, in which the deviation of the sample average from its expectation is divided by the standard deviation of the sample average:

\[Z = \frac{\bar Y - \operatorname{E}(\bar Y)}{\sqrt{\operatorname{Var}(\bar Y)}}\;.\]

Recall that the expectation of the sample average is equal to the expectation of a single random variable ($\operatorname{E}(\bar Y) = \operatorname{E}(Y)$) and that the variance of the sample average is equal to the variance of a single observation, divided by the sample size ($\operatorname{Var}(\bar Y) = \operatorname{Var}(Y)/n$). Consequently, one may rewrite the standardized sample average in the form:

\[Z = \frac{\bar Y - \operatorname{E}(Y)}{\sqrt{\operatorname{Var}(Y)/n}}= \frac{\sqrt{n}(\bar Y - \operatorname{E}(Y))}{\sqrt{\operatorname{Var}(Y)}}\;.\] The second equality follows from placing in the numerator the square root of $n$ which divides the term in the denominator. Observe that with the increase of the sample size the decreasing difference between the average and the expectation is magnified by the square root of $n$.

The Central Limit Theorem states that, with the increase in sample size, the sample average converges (after standardization) to the standard Normal distribution.

Let us examine the Central Normal Theorem in the context of the example of the Uniform measurement. In Figure 10.3 you may find the (approximated) density of the standardized average for the three sample sizes based on the simulation that we carried out previously (as red, green, and blue lines). Along side with these densities you may also find the theoretical density of the standard Normal distribution (as a black line). Observe that the four curves are almost one on top of the other, proposing that the approximation of the distribution of the average by the Normal distribution is good even for a sample size as small as $n=10$.

However, before jumping to the conclusion that the Central Limit Theorem applies to any sample size, let us consider another example. In this example we repeat the same simulation that we did with the Uniform distribution, but this time we take $\mathrm{Exponential}(0.5)$ measurements instead:

exp.10 <- rep(0,10^5)
exp.100 <- rep(0,10^5)
exp.1000 <- rep(0,10^5)
for(i in 1:10^5) {
  X.samp.10 <- rexp(10,0.5)
  exp.10[i] <- mean(X.samp.10)
  X.samp.100 <- rexp(100,0.5)
  exp.100[i] <- mean(X.samp.100)
  X.samp.1000 <- rexp(1000,0.5)
  exp.1000[i] <- mean(X.samp.1000)
}

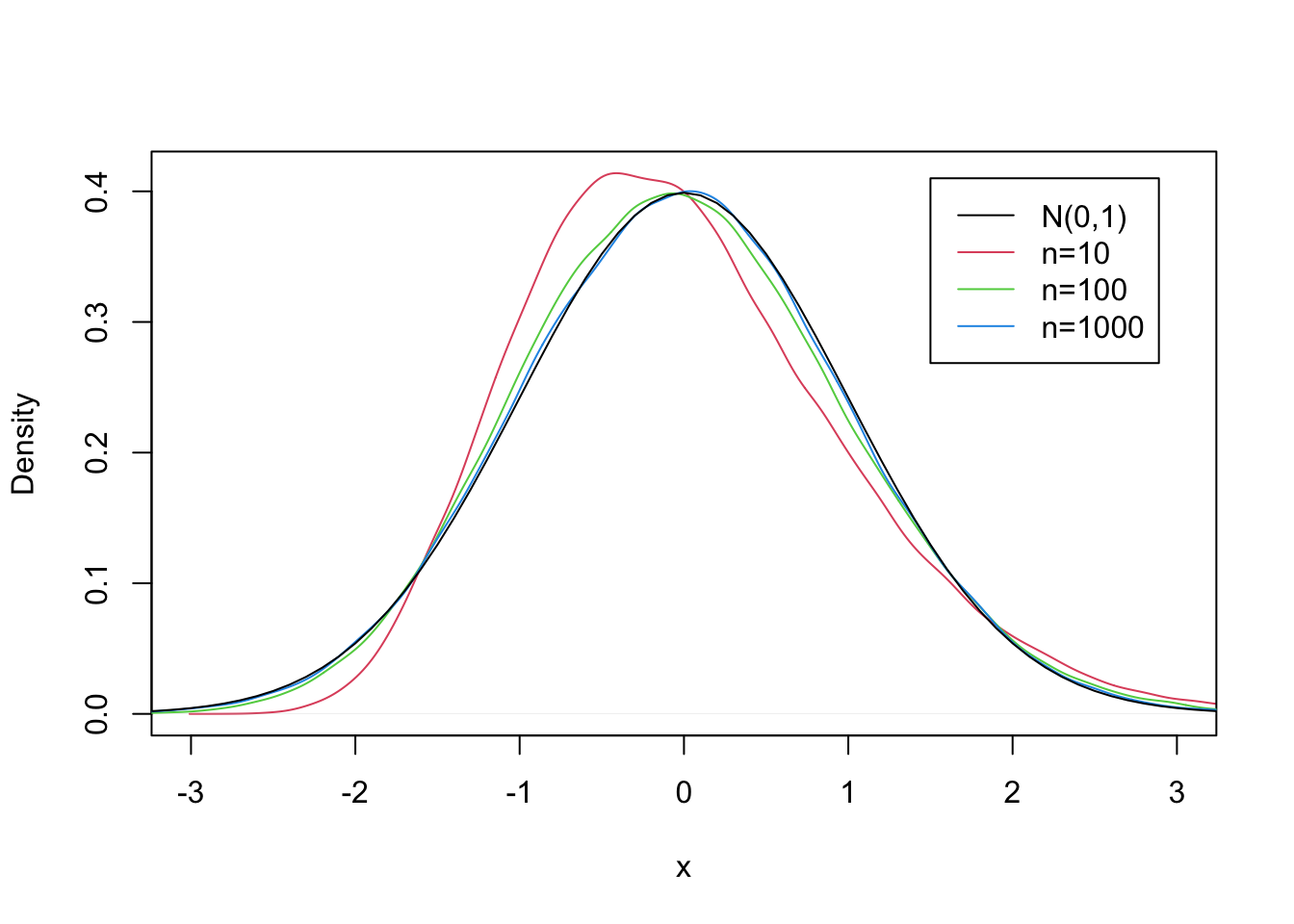
Figure 10.4: The CLT for the Exponential(0.5) Distribution

The expectation of an $\mathrm{Exponential}(0.5)$ random variable is $\operatorname{E}(X) = 1/\lambda = 1/0.5 = 2$ and the variance is $\operatorname{Var}(X) = 1/\lambda^2 = 1/(0.5)^2 = 4$. Observe below that the expectations of the sample averages are equal to the expectation of the measurement and the variances of the sample averages follow the relation $\operatorname{Var}(\bar Y) = \operatorname{Var}(Y)/n$:

mean(exp.10)
#> [1] 1.9974
mean(exp.100)
#> [1] 1.999448
mean(exp.1000)
#> [1] 2.000381

So the expectations of the sample average are all equal to 2. For the variance we get:

var(exp.10)
#> [1] 0.4020298
var(exp.100)
#> [1] 0.04006796
var(exp.1000)
#> [1] 0.003989475

Which is in agreement with the decrease proposed by the theory,

However, when one examines the densities of the sample averages in Figure 10.4 one may see a clear distinction between the sampling distribution of the average for a sample of size 10 and the normal distribution (compare the red curve to the black curve. The match between the green curve that corresponds to a sample of size $n=100$ and the black line is better, but not perfect. When the sample size is as large as $n=1000$ (the blue curve) then the agreement with the normal curve is very good.

10.3.3 Applying the Central Limit Theorem

The conclusion of the Central Limit Theorem is that the sampling distribution of the sample average can be approximated by the Normal distribution, regardless what is the distribution of the original measurement, but provided that the sample size is large enough. This statement is very important, since it allows us, in the context of the sample average, to carry out probabilistic computations using the Normal distribution even if we do not know the actual distribution of the measurement. All we need to know for the computation are the expectation of the measurement, its variance (or standard deviation) and the sample size.

The theorem can be applied whenever probability computations associated with the sampling distribution of the average are required. The computation of the approximation is carried out by using the Normal distribution with the same expectation and the same standard deviation as the sample average.

An example of such computation was conducted in Subsection 10.2.3 where the central interval that contains 95% of the sampling distribution of a Binomial average was required. The 2.5%- and the 97.5%-percentiles of the Normal distribution with the same expectation and variance as the sample average produced boundaries for the interval. These boundaries were in good agreement with the boundaries produced by the simulation. More examples will be provided in the Solved Exercises of this chapter and the next one.

With all its usefulness, one should treat the Central Limit Theorem with a grain of salt. The approximation may be valid for large samples, but may be bad for samples that are not large enough. When the sample is small a careless application of the Central Limit Theorem may produce misleading conclusions.

10.4 Exercises

A subatomic particle hits a linear detector at random locations. The length of the detector is 10 nm and the hits are uniformly distributed. The location of 25 random hits, measured from a specified endpoint of the interval, are marked and the average of the location computed.

What is the expectation of the average location?⁶⁶

What is the standard deviation of the average location?⁶⁷

Use the Central Limit Theorem in order to approximate the probability the average location is in the left-most third of the linear detector.⁶⁸

The central region that contains 99% of the distribution of the average is of the form $5 \pm c$. Use the Central Limit Theorem in order to approximate the value of c.⁶⁹

10.5 Summary

Glossary

Random Sample:: The probabilistic model for the values of a measurements in the sample, before the measurement is taken.
Sampling Distribution:: The distribution of a random sample.
Sampling Distribution of a Statistic:: A statistic is a function of the data; i.e. a formula applied to the data. The statistic becomes a random variable when the formula is applied to a random sample. The distribution of this random variable, which is inherited from the distribution of the sample, is its sampling distribution.
Sampling Distribution of the Sample Average:: The distribution of the sample average, considered as a random variable.
The Law of Large Numbers:: A mathematical result regarding the sampling distribution of the sample average. States that the distribution of the average of measurements is highly concentrated in the vicinity of the expectation of a measurement when the sample size is large.
The Central Limit Theorem:: A mathematical result regarding the sampling distribution of the sample average. States that the distribution of the average is approximately Normal when the sample size is large.

Summary of Formulas

Expectation of the sample average:: $\operatorname{E}(\bar Y) = \operatorname{E}(Y)$
Variance of the sample average:: $\operatorname{Var}(\bar Y) = \operatorname{Var}(Y)/n$

9 The Normal Random Variable

11 Parameter Intervals